6.8.2 转换方案

我们假设Prolog DCG系统有可能通过将DCG规则放入一对大括号来把它和“正常”Prolog文本穿插在一起，并且当 member(E,L)中E是L的元素时底层Prolog系统可以成功定义E。非终结符A到一组DCG取消规则的转换方案由三个部分组成，一个是用于A → Bα形式的规则，一个是用于A → tα形式的规则，以及一个用于处理*$$\overline{A}$$*的特定规则：

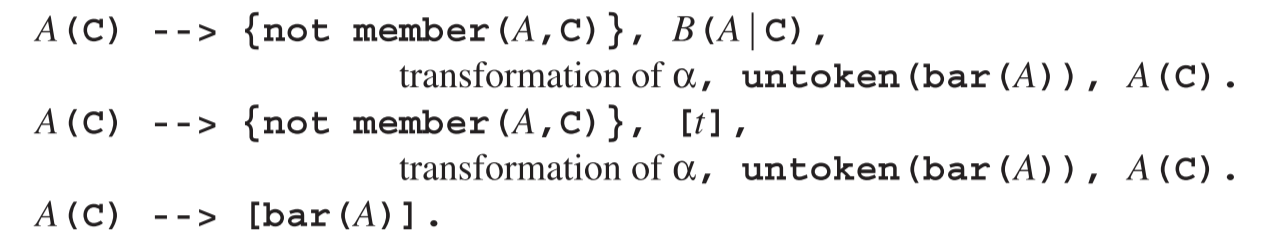
此时，我们假设α不为空；A → ε的并发形式我们下一节再讨论。

这个转换方案包含了很多微妙之处。逻辑参数C是取消集，并且目标**not member(A,C)**暗含了A是否属于取消集的测试。右手侧的转换遵循第6.7.2节中所示的CF-DCG转换，除非所有非终结符都将取消集作为参数。如果右手侧以一个非终结符作为开头，则该非终结符会有一个与A扩展所得的一样的取消集；而其他非终结符都会得到空的取消集。

DCG形式的untoken(bar(A))将$$\overline{A}$$*的一个副本推回输入流。它的工作原理如下：Prolog谓词untoken*定义如下：

untoken(T,S,[T| S]).

DCG处理器会将DCG应用程序untoken(a)开发成Prolog式的untoken(a,Sentence,Remainder)。因此调用untoken(a,Sentence,Remainder)将会给 [a| Sentence]设置Remainder，因此在输入的其余部分的前面加上a。

在A(C)的模式这点上我们已经识别了一个Bα或tα，并将其简化为*$$\overline{A}$$后推回；因此就输入而言我们没有取得任何进展，反而依然有一个A需要解析，但这就是调用方所想要的。这个解析过程必须能从输入中获取$$\overline{A}$$并将其合并到解析树中。$$\overline{A}$$有两个备选项：A 的左递归规则以及 A(C)的调用者。第一种情况下，将在左支构建一个新的A节点；在第二种情况下，A节点的左支就在此处结束。Prolog系统必须同时考虑到这两种情况。这可以通过引入A_x（通过A的所有左递归规则和 $$\overline{A}$$ 来定义）来实现。 此外，为了允许激活新的做递归规则，必须在不显示调用A的情况下调用A_x*。所以我们现在的转换方案是：

其中 *A_l*代表 A的所有左递归规则，以及 A_n代表A的所有非左递归规则。

只要输入前面有一个 $$\overline{A}$$ ，唯一可以往下进展的规则就是可以吸收 $$\overline{A}$$ 的那些规则。其中之一是 A_x(c)-->A_l(c) ，另一个则是第一种模式下的 B。这个B通常与A相等，但如果A是间接左递归那么则不一定是相等的；在这种情况下，对B的调用实际上是调用A_l。如果B等于A，则它在转换过程中的替换必须能够吸收 $$\overline{A}$$，且必须能继续解析A的非左递归实例。所以我们还需要一个A_b，定义如下：

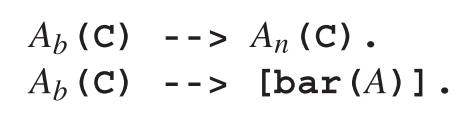
一开始围绕在我们周围的谜团可以通过一个简单的观察来解决：我们可以将A的非左递归规则加到 _A中，而左递归规则加到A_b中，两者都不会影响解析器工作，原因如下。A的非左递归规则永远都不能吸收 $$\overline{A}$$，因此将它们加到A_x中最多导致调用失败；并且对A的左递归规则的调用将会被A_b的左递归检查堵塞。因此A_x和A_b都变成了A_t，定义如下：

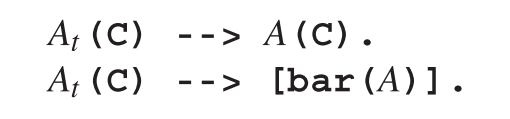
除了简化转换方案外，这还解决了确定哪些规则是左递归规则的需要。

简化后的转换只留下了A和 A_t，其中A_s只能出现在右手侧的非第一个位置。在这些位置，A_s都可以用A_ts替换而没有任何影响，因为唯一的区别是A_t可以接受 $$\overline{A}$$，而 $$\overline{A}$$s不会自行出现在输入中。所以最终在转换模式中只留下了A_ts，这意味着可以重命名为A。这就回到了本节开头的转换方案。

图Fig 6.17展示了图Fig4.1的简单数学表达式语法的结果取消解析器。注意：

expr([expr|C]), [’+’], term([]),，第一个expr是代表DCG，第二个expr只是一个常量，用来添加到取消集中。

我们不是在逻辑变量中构建解析树，而是使用print语句来生成它；由于这些被放置在识别的末尾，因此解析树是按自底向上的方向生成的。使用查询 expr([],[i,’×’,i,’+’,i,’×’,i],[]) 运行此DCG取消解析器会产生以下反向最右派生：