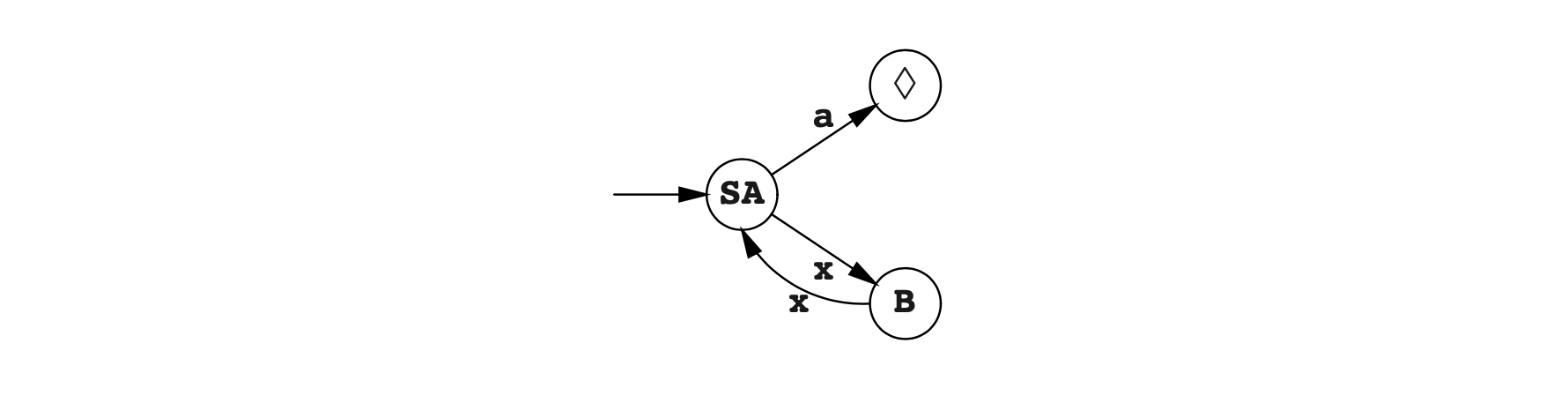
5.7 最小化有限状态自动机

将NFA转换为DFA通常会在自动机中增加大概10个左右的因子，因而使得自动机变得更大，甚至偶尔会使自动机严重膨胀。考虑到对于大型自动机来说，一个10个数量左右的因子增长可能就是一个大问题了；即使是一个小的表格，如果需要存储在一个小型电子设备中，那么任何大小的增加都是难以接受的；但是大尺寸的因子增加的出现是难以预料的，因此很有必要尝试减少DFA中的状态数量。

此处介绍的DFA最小化算法的关键思想是，在我们看到差异之前我们都将状态视为等效状态。因此该算法将DFA状态保存为多个互不相交的子集（“分区”）。一个集合S的分区是S的子集的集合，S的每个元素会处于某个子集中；也就是说，S被划分为互不相交的若干个子集。该算法使用迭代的方式划分子集，根据状态的不同来进行划分。

我们使用图Fig5.23（b）的DFA为例；它可以通过图Fig5.23（a）中的NFA生成，通过A = SQ和B = P算法子集，并且不是最小子集，如我们所见。

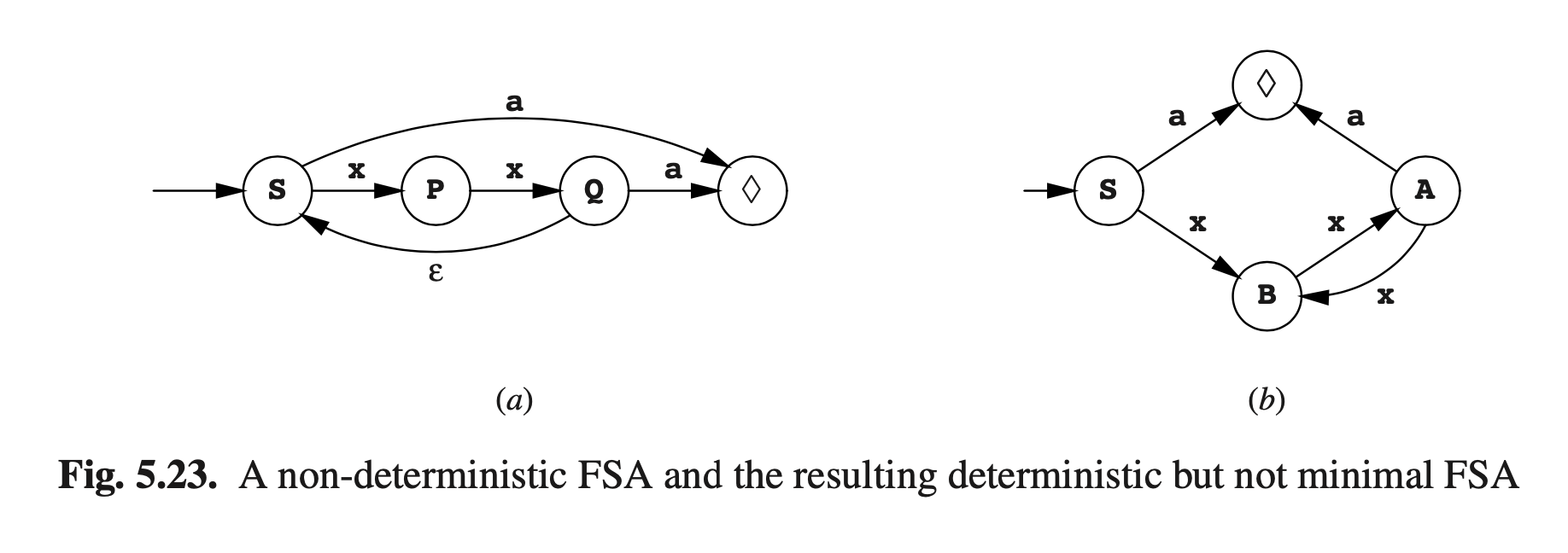
最初我们将状态集氛围两个子集：一个包含所有可接受状态，另一个包含所有其他状态；这些肯定是不同的。在我们的示例中，这将带来一个包含状态S，B和A的子集，以及一个包含可接受状态♦的子集。

接下来，我们反过来在处理每个子集S_i。如果S_i存在两个状态q₁和q₂，则在某些符号上，a已经转换到现在分区的不同子集的元素上，如此我们找到了不同处那么S_i就必须分离出来。假设我们有q₁$$\stackrel{a}{\to }$$r₁和q₂$$\stackrel{a}{\to }$$r₂，而r₁属于子集X₁ r₂属于不同的子集X₂，那么S_i必须被拆分为包含q₁和S_i中其他所有状态q_j（其中满足q_j$$\stackrel{a}{\to }$$r_j，且r_j包含于X₁）的子集，以及另一个包含其余所有来自于S_i的状态的子集。如果q₁在a上没有转换但*q₂有（或者反过来），那我们也能发现不同，并且S_i*依旧要被分割。

在我们的例子中，状态S和A在a上存在转换（指向相同状态，♦），但是状态B并没有，因此这个步骤将生成两个子集，一个包含状态S和A，另一个包含状态B。

我们重复将此步骤应用于分区的所有子集，直到不能在拆分为止。最终一定会是这样，因为子集的数量是有限的：分区中的子集不会比原始DFA中的状态多，并且在整个过程中不会出现合并子集的情况。（这是闭包算法的另一个示例。）

完成这个过程后，生成的分区的子集S_i中的所有状态都有以下属性，对于任何字母符号a它们关于a的转化结束于分区的相同子集S_i(a)。因此，我们可以认为每个子集是最小化DFA的一个单一状态。最小化DFA的起始状态由包含原始DFA起始状态的子集表示，而最小化DFA的可接受状态由包含原始DFA可接受状态的子集表示。事实上，生成的DFA即为识别我们开始使用的 DFA 指定的语言的最小 DFA。见Hopcroft and Ullman [391]。

在我们的示例中，我们已经无法在进行拆分，结果DFA如下图所示。