2.4.1 短语结构案例
直到现在,我们用语法只生成了一个句子,一个特定的时尚,不过语法的目的是生成所有句子。幸运的是还有系统可以做到这个。我们用anbncn语法来做例子。我们从起始符号开始,然后用系统尝试所有可能的替换来生成所有的句子形式;我们只需要等着看哪些句子在什么时候演变成句子。手动完成10个句子试试。如果我们不小心,很容易就会生成像aSQ, aaSQQ, aaaSQQQ,...这样的形式,而且我们将永远也看不到一个完整的句子。原因是我们太过专注于一个单一的句子形式:我们应该给所有的句子同样的时间。这可以通过下面的算法完成,其保持句子形式的一个队列(也就是一个列表,表中是我们要加到结尾和从开头删除的元素)。
从起始符号开始,作为队列中唯一的句子形式。现在继续以下操作:
- 考虑队列中的第一个句子形式。
- 从左到右扫描它,寻找符合左侧生成规则的字符串。
- 发现的每一个这样的字符串,复制足够的句子形式,替换每一个符合左侧生成规则的字符串,通过规则中不同的选项,然后把它们全部添加到队列末尾。
- 如果原始句子形式不包含任何非终结符,把它作为语言中的一个句子写下来。
- 扔掉原始的句子形式;它已经被处理完成了。
如果没有匹配的规则,并且句子形式不是一个完成的句子,那这就是一条死胡同;它们会被上述过程自动删除,不留任何痕迹。
因为上述过程枚举了PS语言中所有的字符串,PS语言也被称为递归可枚举集,这里的“递归”是指“通过一个可行的递归算法”。
图Fig 2.7中anbncn语言的处理过程的开始几步,展示在图Fig 2.17中。队列向右运行,其第一项在左侧:
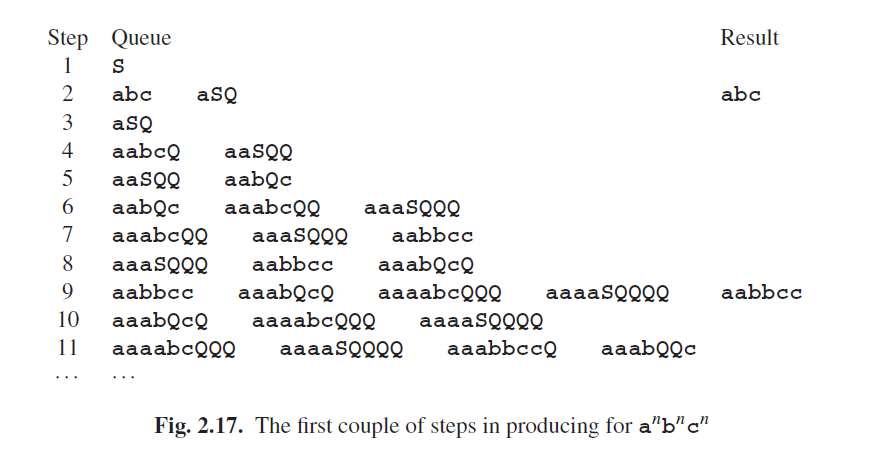
可以看到,并不是每次我们打开曲柄都可以得到一个句子;实际上,在这种情况下真正的句子十分稀少。当然是因为在这一过程中,发展出了很多的侧边线,而这都需要同等的重视。不过我们可以肯定,每一个可以生成的句子最终都会生成:我们不会放过任何可能。这种方式被称为广度优先生成;而计算机做的比人要好。
很容易认为对我们在顶层句子形式中发现的所有左侧内容全部替换是不必须的。为什么不只替换第一个,然后等下一个句子形式出现,在替换下一个?然而这是错误的,因为替换第一个有可能会导致第二次替换时上下文混乱。一个简单的例子就是下面的语法:
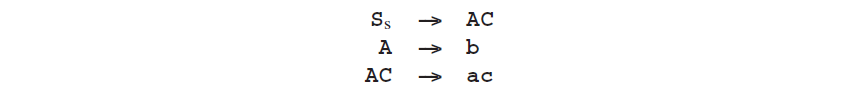
第一次替换A--->b将会走到死胡同里,那语法将什么也不会生成。做两个可能的替换也将导致同样的死路,但是却依旧会有第二个句子形式,ac。也有一个语法例子,其中队列在一段时间(很短)后将会变空。
如果语法是上下文无关的(或正则),那就不会有所谓的上下文被破坏了,那么替换第一个(或只替换)匹配的就是很安全的了。
这里有两点要说明。第一,经过我们努力之后得到的句子并不一定就会是我们想要的那个:很可能每一个新的句型又包含着一个非终结符。我们应该通过检查语法事先知道,不过可以证明对PS语法来说是不可能做到的。形式的语言学家(formal-linguist)说“一个PS语法是否生成空集是不可判定的”,这意味着,没有一个算法能明确得出每一个PS语法最终是否能生成一个句子。不过这不意味着我们不能对于给定的算法证明其无法生成句子,如果该语法是这样的情况。这意味着证明方法不适用于所有的语法:在一定时间内能完成那我们就可以有一个程序,而如果是不能完成的那时间就无法估测了。实际上,上述生成过程就是一个确切告诉我们答案是“是\否”的算法(虽然我们可以有一个告诉我们“是\不知道”的算法,在有限时间内)。虽然由于语言的一些深层属性导致我们不能总是确切得到我们想要的答案,但这并不会妨碍我们获取各种信息以更加了解语法。我们应该看到这是一种反复出现的现象。计算机科学家知道形式语言学的绝境,但他们并不气馁。
第二点是,当我们确实从上述生成过程中得到句子的时候,它们却可能是通过不可探寻的顺序生成的。对于非单调语法,句子形式可能短暂增加然后急剧缩小,甚至可能变成空字符串。形式语言学证明,不会有一个适用所有PS语法的算法来生成长度增加(实际上是“非递减”)的句子。换句话说,PS语法的解析问题是不可解决的。(虽然术语是可以互换的,但似乎使用“不可判定”来描述“是\否”问题以及“不可解决”来描述“解析问题”要更合理。)