2.7.1 uvwxy理论
当我们从CF语法中获得了一个句子后,我们应该仔细看句中的每一个终结符,然后问自己:它是怎么在这的?然后看一下生成树,我们看到它被生成作为右侧规则m的第n位成员。这个规则的左侧,符号的父节点,再次生成规则Q的第p位成员,等等,直到我们到达起始符号。在某种意义上,我们可以通过这种方式追踪符号的轨迹。如果一个符号的轨迹的所有规则/成员对都是不同的,我们称这个符号是原始的,如果一个句子中的所有符号都是原始的,我们称这个句子是“原始”的。
例如,下面生成树中第一个h:
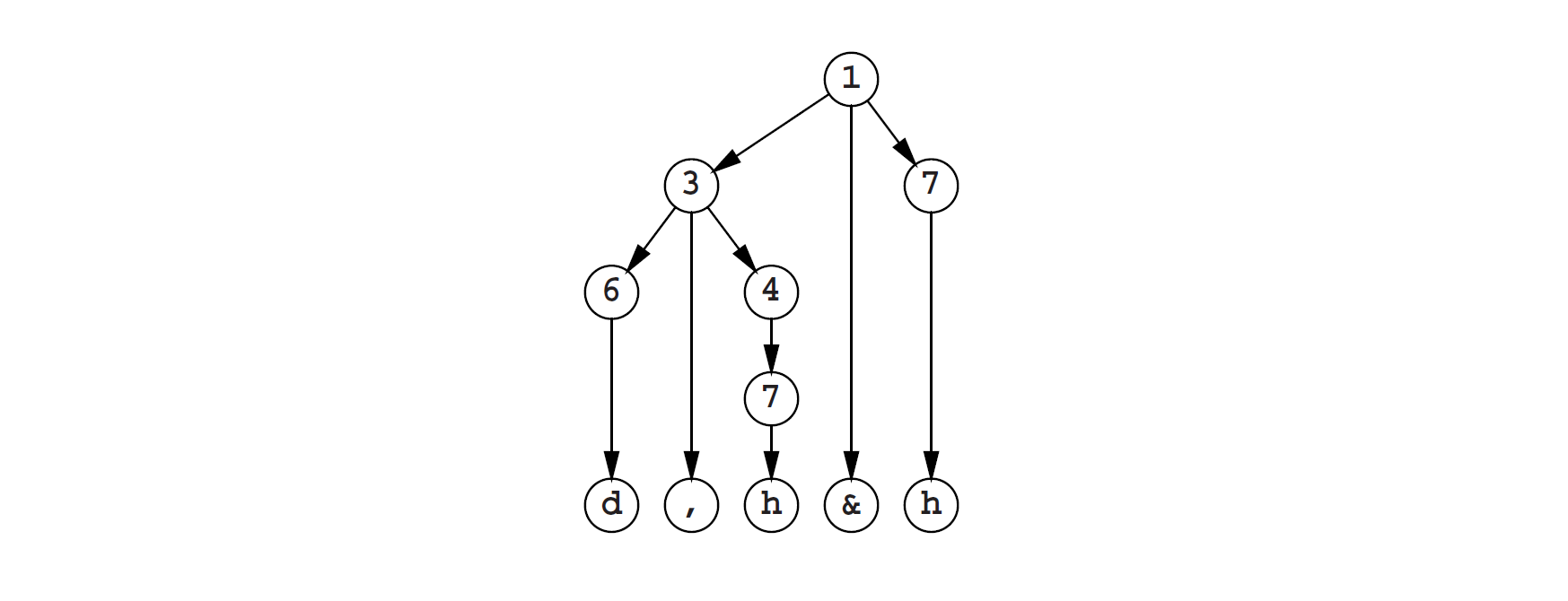
由下面语法生成的

h的谱系是,来自7,1,来自4,1,来自3,3,来自1,1.这里,第一个数字代表规则数,第二个数字代表这个规则中的成员数。因为所有的规则/成员对都是不相同的,所以h是原始的。
现在对于一个给定的符号,只有有限的方式来让其是原始的。这很容易,如下所示。一个原始符号的谱系中的所有规则/成员对必须是不相同的,所以其谱系的长度一定不会比语法中所有不同规则/成员对的总长度还长。 There are only so many of these, which yields only a finite number of combinations of rule/member pairs of this length or shorter. 理论中,一个符号的原始谱系的数量可能是非常巨大的,但实际中确实非常小的:如果有超过10种方法来生成一个给定的符号,从语法中通过原始谱系,那这个语法将会是非常错综复杂的!
这对原始句子就有了严格的限制。如果原始句子中一个符号出现两次,这两个的谱系必须不相同:如果谱系相同,那它们应该描述的是用一个位置的同一个符号。这意味着原始长度有着最大长度:所有符号的原始谱系的长度总和。对一个编程语言语法的平均的长度,在数以千计的符号的长度顺序中,大致相当于语法的长度。所以,因为有着最长的原始句子,那么就只能有着有限数量的原始句子,然后我们就得到了一个令人惊讶的结论就是任何CF语法只生成大小有限的原始句子核心,以及(也许)无限数量的非原始句子!
“非原始”句子是什么样的?这就是我们开始介绍uvwxy定理的地方。一个非原始句子具有这一的属性,在谱系中包含至少一个重复出现的符号。假设那个符号是q,重复的规则是A。那我们就可以画一幅类似图Fig2.21的图,w是由A的最新应用生成的部分,vwx是A的其他应用生成的部分,uvwxy就是这个非原始句子。现在我们立即就可以找到另一个非原始句子,通过删除以A为顶点的小三角,然后用以A为顶点的大三角副本替换;见图Fig 2.22。
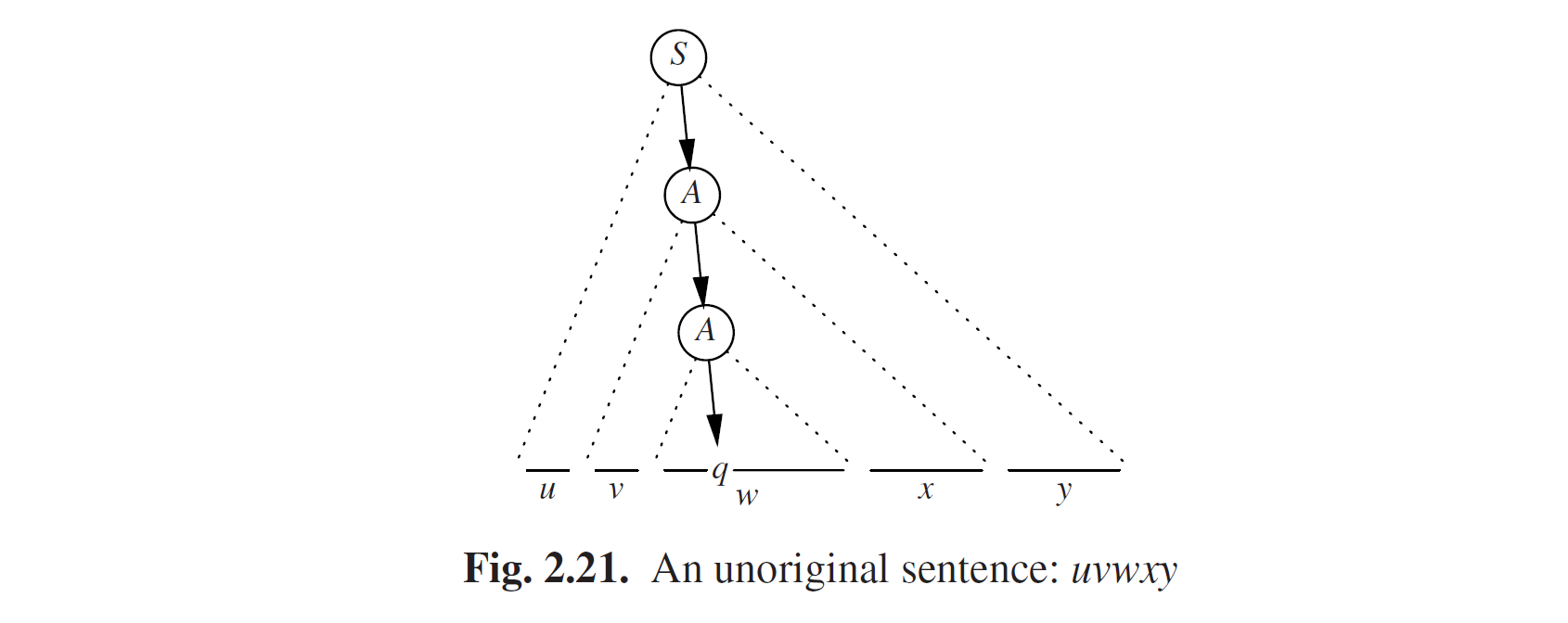
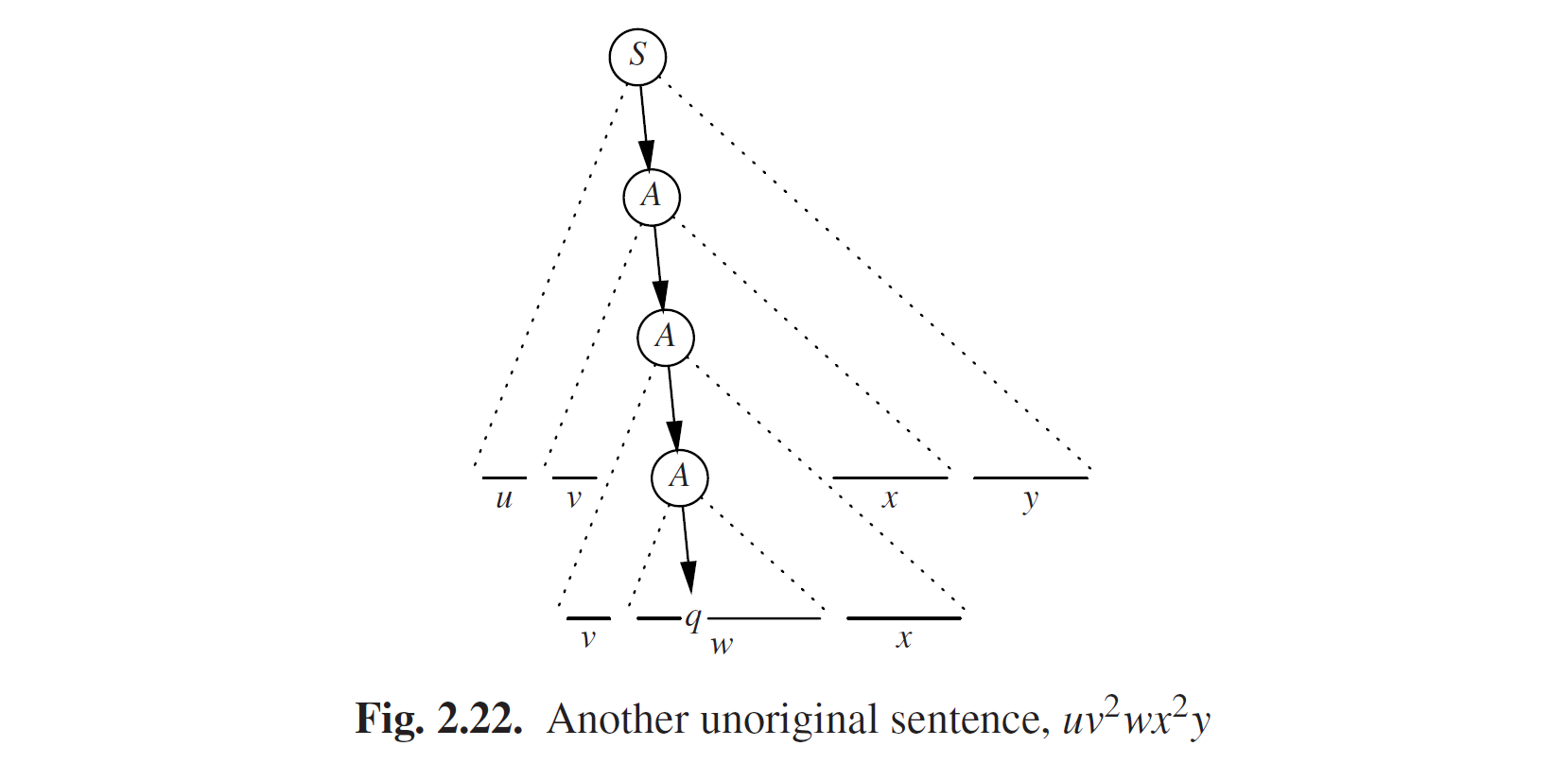
这个新的树生成了句子uvvwxxy,并且以这种方式,可以很容易看到我们能构建句子uvnwxny的完整家族对于所有n ≥ 0的。这种方式显示了w嵌套于一组v和x括号之间,在u和y无关的上下文中。
底线是当我们审查一个上下文无关语言中的越来越长的句子,原始句子慢慢用尽,我们遇到的只是句子的相近形式的家族,慢慢缩进至无限。这在uvwxy理论中有总结:任何由CF语法生成的句子,比最长的原始句子还要长的句子,都可以被切分称五个部分u,v,w,x,y,以这种方式uvnwxny就是这个语法下n ≥ 0得来的一个句子。uvwxy理论也被称为上下文无关语言的泵引理(pumping lemma),而且由几个变种。
有两点必须在这里指出。第一点,如果一个语言持续生成越来越长的句子,而不减少嵌套句子的族系,那这个语言就不会存在一个CF语法。我们已经遇到了上下文相关语言anbncn,很容易看到(但不是很容易去证明!)它不会衰退成这样的嵌套的句子,当句子变得越来越长时。因此,它是没有CF语法的。这种证明的通用技术见Billington [396]。
第二点是,最长的原始句子是语法的一个属性,而不是语言的。通过为语言制造一个并发的语法,我们能增加原始句子的集合,并且可以推开我们被迫诉诸于嵌套部分的边界。如果我们让语法无限并发,那我们就能使边界变得无限,并从中获得一个短语结构语言。如何将CF语法变得无限并发,将会在15.2.1节中的两级语法中介绍。