4.3 表解析
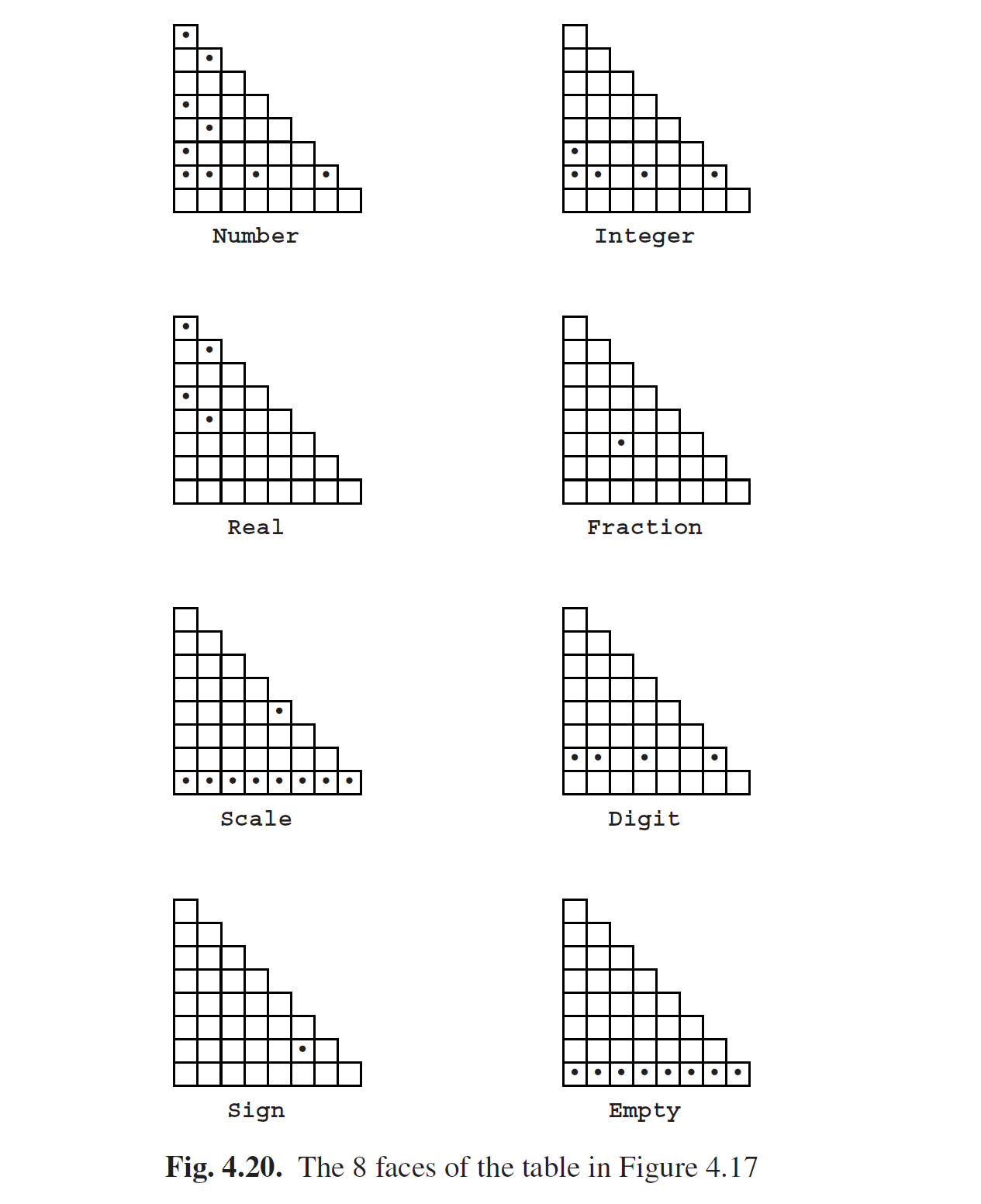
前面我们已经将CYK识别表绘制成了一个二维三角矩阵,但输入内容(非终结符集合)的复杂性已经表明,这并不是最原始的形式。通过发现CYK识别表是多个表(语法中每个非终结符都是一个表)的叠加可以更简洁有深度;这些输入内容在这些表里面只是位(bits),含义是“Present”或者“NotPresent”。由于图Fig4.6中的数字语法有8个非终结符,因此图Fig4.17的识别表就是8个矩阵的叠加。见图Fig4.20。Number表左上角的点表示一个长度为7的Number已经识别到了位置1;在差不多最右下角的一个点表示一个长度为1的Number已经被识别到了位置7;以此类推。
想象一下,这8个表就以Number · · · Empty的顺序,分隔成一个个单元,然后以队列加入一个单独的块中(block)。现在将这个块的顺序颠倒过来。就有了一个新的矩阵T,原本的底部成为了现在的顶部,如图Fig4.21,新表的x轴的位置不变,但y轴变成了非终结符的名称和输入句子的长度。例如,左上角*T1,Number*中的数组{1,2,4,7}表示Number的长度为这些的生成结果放在位置1。以这种方式为主的解析算法,称为表解析算法(tabular parsing algorithms)。很明显,在此转换中,不会新增或删除任何信息,但表解析也有自身的优势和不足。


表T在将1放入所有输入Ti,A(输入中有一个令牌T位于位置i,且语法为A→t)时进行初始化。有两个方法可以填充表的剩余部分,自顶向下和自底向上。