5.3.2 ε转换和非标准符号

标准形式的正则语法只会有A → a和A → aB的形式。我们先来用另外两种规则A → B和A → ε扩展一下符号，然后看看如何为他们构造NFAs和DFAs。接下来我们看看正则表达式和以正则表达式作为右侧的规则（例如P → a^∗bQ），并展示如何将他们转换加入规则的扩展符号中。

图Fig5.14的语法包含两种新类型规则的例子；图Fig5.15展示了这个语法的三剑客：NFA，状态树和DFA。先看NF，当我们出于状态S的时候，我们会在令牌a处转换到预期状态B，最终得到标准规则S->aB。非标准规则S->A表示我们可以从状态S到状态A，而不需要读取（或生成）符号；即我们读取一个长度为0的ε字符串，并且做了一次ε转换（或ε转移）；S $$\stackrel{\xi }{\to }$$ A。非标规则A->ε产生一个ε转换以得到可接受状态：A $$\stackrel{\xi }{\to }$$ ♦。ε转换不能和ε规则混淆：单元规则产生ε转换得到不可接受状态，而ε规则产生的ε转换得到可接受状态。

现在我们已经构建了一个具有ε转移的NFA，现在的问题是我们如何处理ε转移以得到DFA。为了解决这个问题，我们像前面一样推导；在图Fig5.7中，在看到a之后我们并不知道现在是出于状态A还是B，我们将之记为 {A, B}。此时当我们进入状态S时，甚至在处理单个符号之前，我们就已经不知道我们是处于状态S还是A或者 ♦了，由于后两者都可以通过ε转移由S到达。所以DFA的初始状态已经是复合的：SA♦。我们必须考虑此状态将会把符号a和b指向什么地方。如果是状态S，a将指向B，然后如果是A那么a将指向A。因此新状态包含A和B，而由于 ♦可以由A通过ε转移到达，因此它也包含 ♦且命名为AB♦。继续这条路径，我们可以构建完整的状态树（图Fig5.15(b)），折叠起来就成了DFA（c）。注意，DFA的所有状态都包含NFA的状态**♦**，因此输入可能以其中任何一个结束。

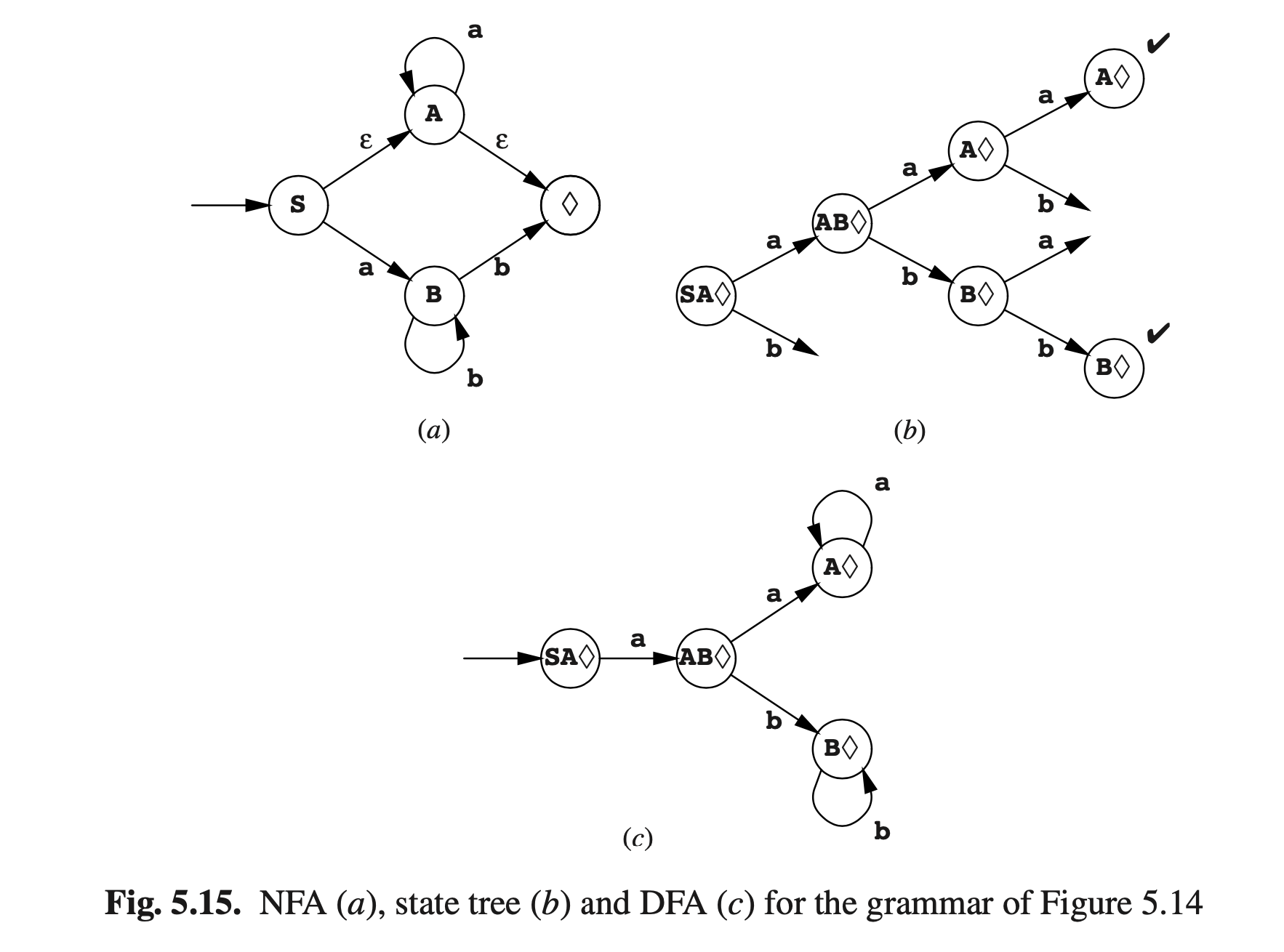
通过a的给定状态由ε转移得到NFA状态的集合称为那个状态的ε闭合。例如S的ε闭合是 {S, A, ♦}。

有关从最近发现在 XML 验证领域的正则语法获取 DFA 的完全不同方法，请参阅 Brzozowski [139]。