2.1.3 无限集带来的问题
上述将语言定义为序号序列的无限集,将语法定义为有限的构造句子的配方,这引出了两个令人尴尬的问题:
1.一个有限的配方如何能产生无限的句子集呢?
2.如果一个句子只是一个序列而没有结构,或者如果一个句子,可以通过其结构推导出其他的意义,那我们该如何理解这个句子呢?
这两个问题有一个漫长而复杂的答案,不过确实是有答案的。我们先解决第一个问题,然后在带着第二个问题去阅读本书的主体部分。
2.1.3.1 有限描述的无限集
其实从一个有限的描述中得到一个无限集,并没有什么问题:“所有正整数集合”是一个非常有限的描述,但描述的却是一个无限集合。不过,还是有一些令人不安的想法,所以我们把问题换一个说法:“所有的语言都能用有限的描述来说明吗?” 正如上文暗示的,答案是“不行”,不过证明却不是显而易见的。实际上这个证明非常有趣并且有名气,如果不展示一下或者至少大致的介绍一下,将会是一个遗憾。
2.1.3.2 枚举描述
证明基于两个事实,并使用了一个窍门。第一个事实是,描述是能够被逐一列出并赋予一个编号。方法如下。首先,找出全部大小为1的描述,也就是那些长度只有一个字母的,然后将他们按字母顺序排序。这是我们列表的开头。取决于我们所接受的描述,长度为1的描述可能是0,或27(所有字母+空格),或者95(所有可打印的ASCII字符)或者其他类似的;具体是什么对下面的讲解都不重要。
第二步,我们找出长度为2的描述并将他们按照字母顺序排序,然后将他们放在列表中的第二块;然后是长度为3的,长度为4的等等等等,对每一个描述都这样做。这样每一个描述都在列表中获得一个位置。例如“所有正整数的集合(the set of all positive integers)”这个描述,不算引号大小为32个字符(英文)。若要查找其在列表中的位置,先计算有多少少于32字符的描述,记为L。然后生产所有长度为32的描述并排序,然后确定我们的描述在其中的位置,记为P,把L和P加起来。这肯定会是一个巨大的数字1,不过这就能确保我们的描述处于这个列表中了,并且有定义明确的位置;见图Fig.2.1。

有两件事情需要注意。第一,只根据字母表顺序列出全部描述而不指定其长度,将导致以字母‘a’开头的描述就会有无限多个,其他字母开头的描述无法在这个列表中列出来。第二,没有必要将所有的描述实际的列出来,这只是一个思想实验。
当然,列表中会有很多胡言乱语的描述;不过这对我们的论点来说是无关紧要的。重要的是以上的论证能够确保所有有意义的描述都在这个列表中。
一些计算表明,在ASCII-128假设下,这个数字是248 17168 89636 37891 49073 14874 06454 89259 38844 52556 26245 57755 89193 30291,或者大致是2.5× 。
2.1.3.3 语言,无限的比特串
我们知道,一种语言中的单词(句子)是由有限的符号集组成的;这个集合很自然的被称为“字母表”。我们假设字母表中的字母是有序的,那么语言中的单词也能排序。在下文中我们用字母来表示字母表。
最简单的语言就是使用字母表中的字母组成所有单词的语言。对于字母表 = {a,b},我们获得了一门语言{ , }。我们把这个语言称为*,稍后再说为什么这么称呼;现在来说,这只是一个名字。
上面用*标记的集合,以“{ , a,”为开头,值得注意的是,这个语言的第一个单词是一个空单词,这个单词包含0个和0个。没有理由排除这个单词,但如果写下来又很容易被忽视掉,所以我们把这个空单词记为。所以,* = { , }。在一些自然语言中,动词“to be”的现在时态就是一个空单词,赋予“I student”这个句子以“I am a student”的意义。俄语和希伯来语就是很好的例子。
因为字母表中的符号是有顺序的,我们可以列出语言*中的单词,使用上一节中说到的方法:第一,将所有大小为0的单词排序;然后大小为1的单词排序;然后后面依次。实际上我们已经在*中这样做了。
语言*有一个有趣的地方,就是所有使用字母表的语言,都是它的子集。这意味着,在的基础上创建一门不那么复杂的语言,称做,那我们就能遍历*列表中的所有单词,然后在属于的单词上做一个标记。这样就能把中的全部单词都包括了,因为*本来就包括了所有由中的字母组成的单词。
假设所有字母比字母多的单词都属于语言。那么就是这样的{}一个集合。那*列表的开头部分就是下面这样的:

给定一个字母表和他的次序,无标记和有标记的部分就完全足够识别和描述一个语言了。为了方便,我们将无标记的部分写作0,将有标记的写作1,就像计算机中的位(bits)一样,那我们现在就可以把写成 = 0101000111010001· · ·(而* = 1111111111111111· · · )。需要指出的是这适用与任何语言,比如一门形式语言,一门编程语言Java,一门自然语言英语。在英语中,标记为“1”是非常稀少的,因为几乎没有任何一个任意序列的单词组合会是一个有意义的句子(同理,没有任何一个任意序列的字母组合是一个有意义的单词,取决于我们针对的是“句子/单词”级别还是“单词/字母”级别)。
2.1.3.4 对角化
上一节将无限位字符串0101000111010001· · ·和“所有字母比字母多的单词集合”这个描述联系在一起。同样,我们可以将这种位字符串一一对应到所有的描述上。有些描述可能不足以产生一门语言,这种情况下我们可以将任意无限位字符串和他对应。既然所有的描述都可以放到一个被编号的列表中,那么我们就有了下面的图:

左侧是所有的描述,右侧是描述对应的语言。现在我们可以声称很多已经存在的语言却不存在于上述列表中:上述列表远远不够完整,虽然列表的描述是很完善了。为了证明这点,我们将使用Cantor的对角化过程(“Diagonalverfahren”)。
想象一下,语言 = 100110· · ·,它是由这样组成的:它的第n阶位并不等于描述#n中描述的第n阶位。语言的第一个比特位为1,因为描述#1的第一个比特位是0;第二位是0,因为描述#2的第二位是1,等等。是由上图language部分的左上方到右下方的对角线的相反位组成。就是图Fig 2.2(a)中对角线。那语言就不存在于列表中!它不是行1,因为它的第一位不同于(应该说,被弄得不同)行1的第一位,更一般的,通过定义得出,它也不是行n,因为它的第n位与行n的第n位不同。
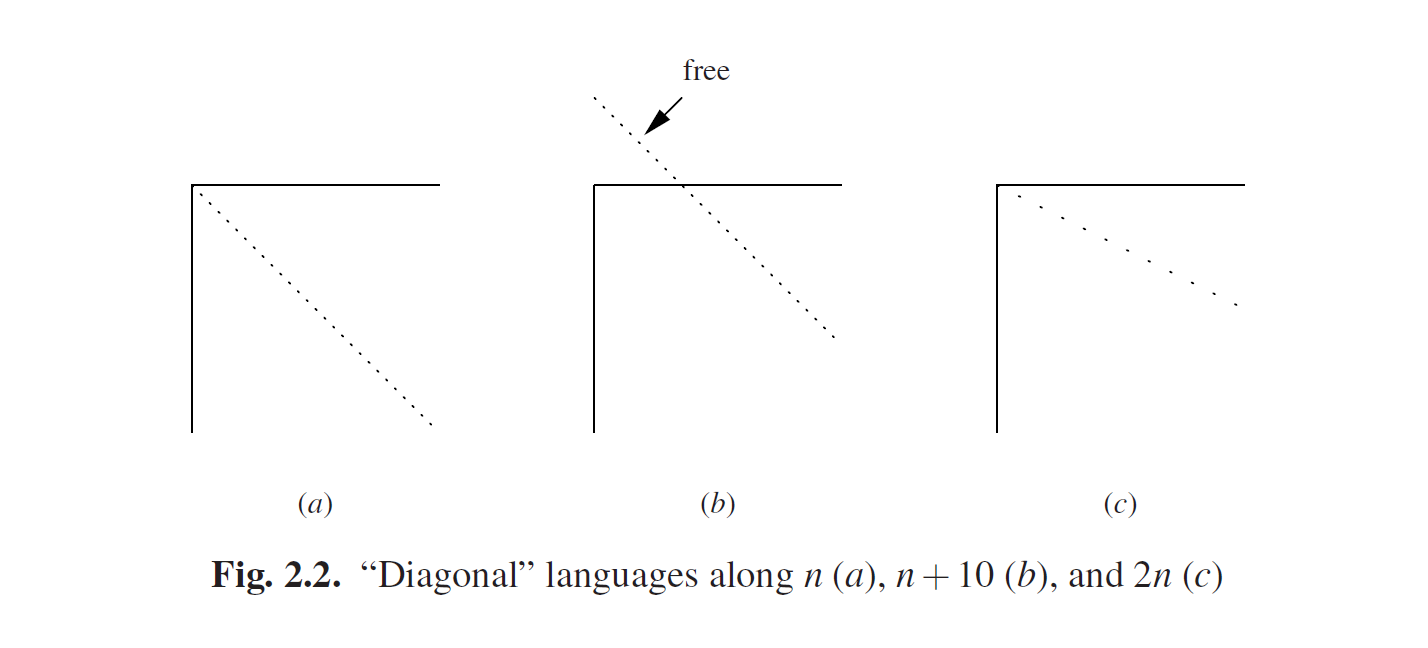
所以,尽管我们已经详尽无遗的列举了所有可能的有限描述,那也至少会有一种语言的描述不在列表中(实际上有很多)。例如,构造一个语言,它的第n+10位与描述#n的第n+10位不同。同样的,这个语言也不在列表中,因为对于任意一个n>0,它的第n+10位与与描述#n的第n+10位不同。这意味着1到9位没起作用,可以任意替代,如图Fig 2.2(b)所示;这将生成另外2 = 512种语言,且都不在列表种。而且我们构造更多!假设我们构建了一门语言,它的第2n位与描述#n(c)的第2 n位不同。明显它也不在原列表中,并且每一个奇数位都没有指定值,而且可以随意选择!这使得我们可以自由的创建无限数量的语言,并且都无法用有限的描述表示;见图Fig 2.2中的斜对角线。简而言之,相对于可以描述的语言来说,还有更多的无法描述的语言。
关于对角化技术,在理论计算机科学中的很多书中有更正式的讲解;例如Rayward-Smith [393, pp. 5-6], 或者 Sudkamp [397, Section 1.4]。
2.1.3.5 讨论
上面的示例表明了几件事情。第一,它展示了把语言当作一个形式对象处理的力量。虽然上述概要仍需要补充很多证据才能成为一个合格的证明。为什么上述语言的定义本身不在描述列表中;见问题2.1,这让我们能深入了解其本质。
第二,这表明我们只能描述所有可能语言的很微小的一部分子集(甚至都不是一小部分):语言的数量是无限的,且远远超出我们能弄清的范围。
第三,我们已经证明,虽然有无穷多的描述和无穷多的语言,但是这两个无穷多却不相等,后者要远大于前者。这些无穷被Cantor称为0和1,而上述只是他对0 1进行证明的一个特殊例子。