5.3.1 用状态替换集合

尽管上述过程在输入长度上是线性的（下一个令牌需要的工作量与长度无关），但是对于每个令牌依旧需要做大量的工作。更糟的是，必须反复查询语法，因此解析的速度会被语法的大小影响。简而言之，我们为非确定性自动机设计了一个解释器，它很方便易懂，但是效率底下。

好在我们有可能从根本上改进它：从图Fig5.7中的NFA中，我们构建了一个新的自动机与一组新的状态集，其中每一个状态都相当于一个旧的状态集。如果原始自动机（非确定性）在第一个a之后不知接下来往哪边（我们用 {A,B}来表示的状态），那么新的自动机（确定性）将明确知道第一个a之后，它的状态就是AB。

新的自动机状态可以系统的构建。我们从旧自动机的初始状态开始，这同样也是新自动机的初始状态。对于我们创建的每个新状态，我们根据旧状态检查其内容，对于语言中的每一个令牌我们决定给定集合导向哪个旧的状态集合。这些旧状态的集合将再次被视为新自动机的状态。如果我们再次撞见相同的状态，它将不会再次被分析。这个过程称为子集构造，并会产生一个（确定性）状态树。图Fig5.6的语法的状态树如图Fig5.11所示。为了强调它系统的检查所有符号的所有新状态，还显示了无向的连接弧线。新生成的但以前就存在的状态用✔标示了。

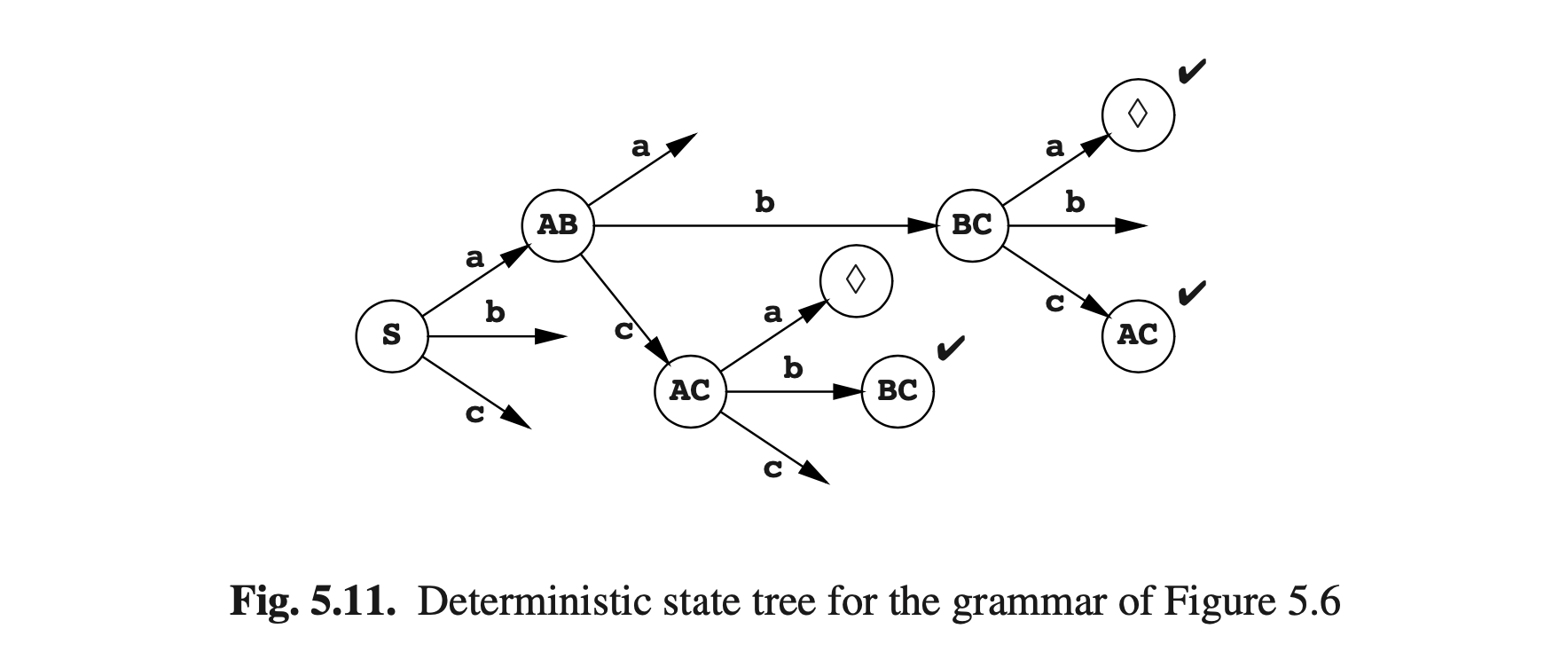
图Fig5.11的状态树通过将箭头指向✔标记过的状态（首次出现的）并删除死角而转变为一个转换图。新的自动机见图Fig5.12。它是确定性的，因此称为确定性有限状态自动机，简称DFA。

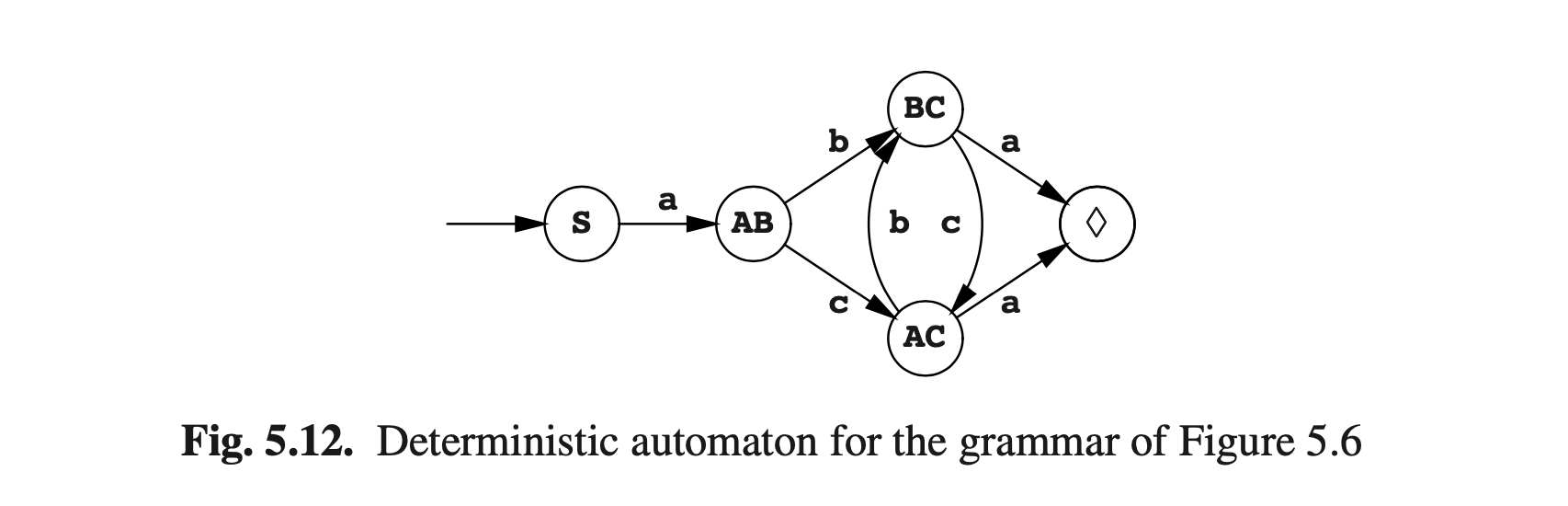
当我们现在使用句子abcba作为遍历此转换图的向导时，就会发现过程中不会产生任何疑惑并且顺利得到可接受状态。状态指出的每一条弧线都带有不通的符号，因此只要遵照符号表，我们始终都只会有一个方向。如果给定一个状态没有给定符号的指出箭头，则该符号可能不会出现在该位置。如果存在，则输入错误。

有两点要注意。首先，我们看到大多数可能的新自动机状态实际上并没有实现：旧状态机有5个状态，所有新自动机有2⁵=32种可能状态，而实际上它的状态只有5种；像SB或者ABC这样的状态不会出现。这很正常，虽然n种状态的非确定性有限状态自动机变成DFA后，理论上有2 ⁿ状态，但是其中有些非常罕见并需要特别的构造出来。具有n种状态的NFA通常会产生少于或约等于10 × n状态的DFA。

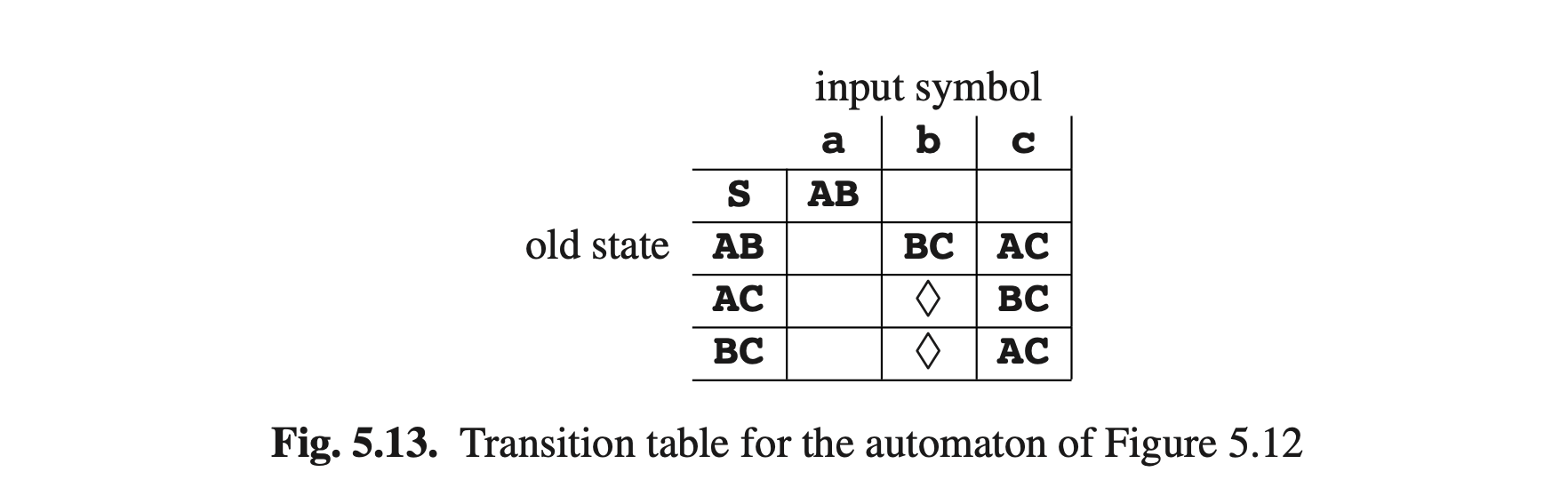
其次，不再需要查询语法；输入令牌的自动机状态完全确定了下一个状态。为了方便查询，下一个状态可以存储在由旧状态和输入令牌索引的表中。DFA的索引表见图Fig5.13.通过这个表，可以以很少的机器指令来完成检查输入字符串的每个令牌。对于大多数DFA，表中的大多数条目为空（无法通过正确的输入到达，并且指向错误状态）。由于表相当的大（300状态的100次方个令牌，是很普遍的大小），不过有几种技术来压缩为空的部分来减小表的大小。Dencker, Dürre 以及 Heuft [338]对这些技术做了一下调研。

获得的解析树如下：

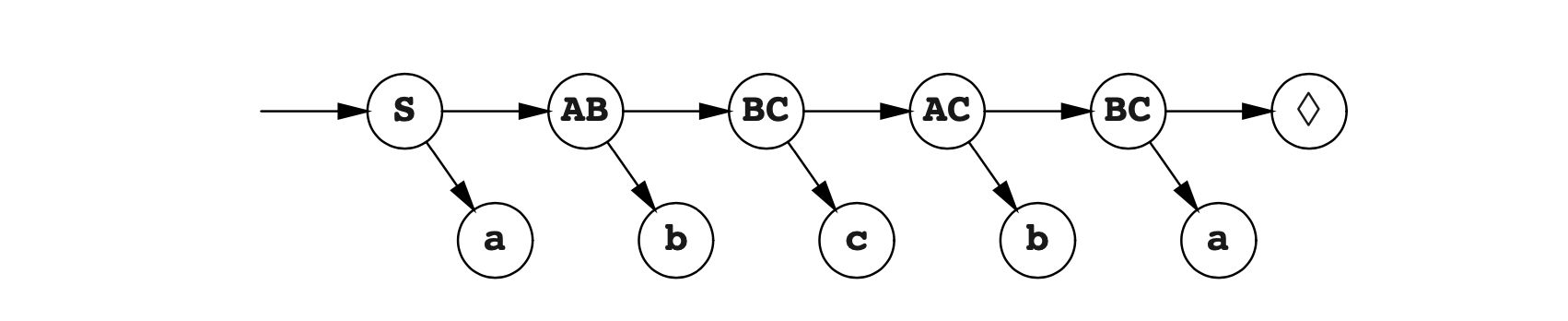
这不是原始的解析树。如果自动机仅用于识别输入字符串，是没有任何问题的。如果需要解析树，可以按照以下自底向上的方法来重建。从最后一个♦状态和令牌a开始，我们得出结论，最后一个右侧（自底向上解析的“句柄段”）是a。由于状态为BC，B和C的组合，我们看一下B和C的规则。我们会发现有一个派生是C->a，它简化了BC到C。最右侧的b和C组合成为句柄bC，其存在与A派生的集合 **{A,C}**中。用这个方式进行之后，我们就得到如下的解析：

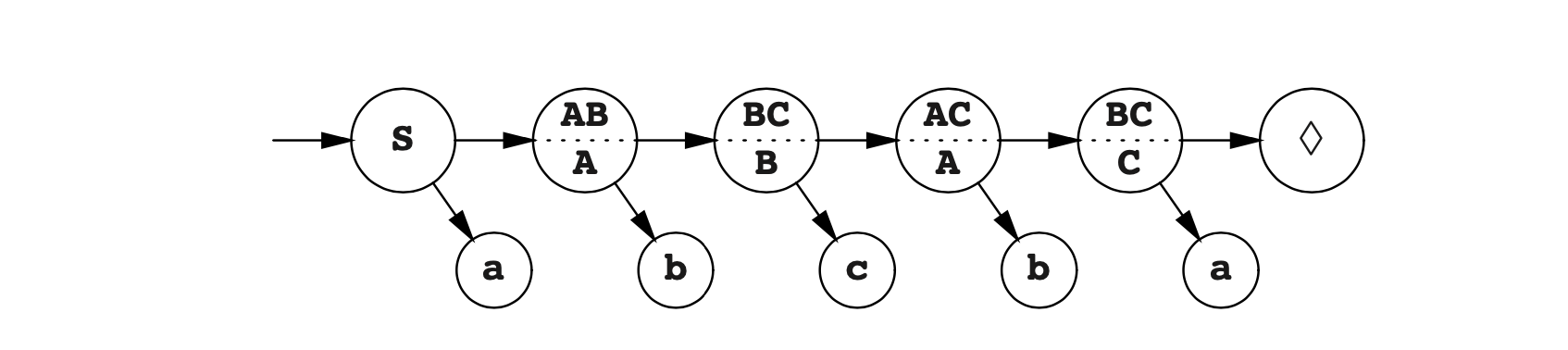
这个方法又会重复查询语法；此外，回退的方式并不总是像上面的例子那么简单，我们将会得到不确定的语法。

对正则语法进行有效的全面解析，关注的人并不多；但是在Ostrand, Paull and Weyuker [144] and by Laurikari [151]的论文中可以找到很多有用的信息。