2.3.1 1型语法
0型语法的特征是,它包含一条规则是可能将任意数目(非零)的符号转化为任意数目(可能为零)的符号。例如:
, N E ---> and N
如上三个符号被两个符号取代。通过限制这种自由,我们引入1型语法。奇怪的是关于1型语法的,直觉上完全不同的两个定义,却很容易被证明是相同的。
2.3.1.1 1型语法的两个类型
如果一种语法它不包含规则,左侧的符号比右侧符号更多,那它就是1型单调,。例如,禁止这个规则 , N E ---> and N.
如果一种语法的所有规则都是上下文相关,那它就是1型上下文相关。上下文相关就是,如果左侧只有一个符号(非终结符)被其他符号替代,然后我们把右侧的符号都找到且没有损坏且按顺序放置。例如:
Name Comma Name End ---> Name and Name End
这就说明这个规则
Comma ---> and
可能适用,如果左侧文字是Name而右侧文字是Name End。上下文本身不受影响。替代者必须是至少一个符号长。这意味着上下文相关语法总是单调的;见2.5节。
这里是t,d&h例子的一个单调语法。在书写单调语法时,必须要小心绝不能多生成一个后面本来就会生成的符号。我们通过将结束标记纳入最右侧的名字来避免需要删除键鼠标记:

当EndName是一个单独的符号时。
这就是它的一个上下文相关语法。
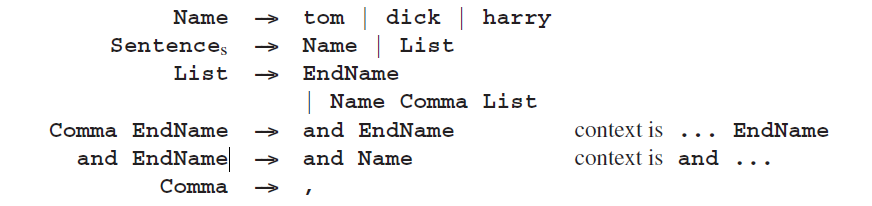
请注意,我们需要一个额外的非终结符逗号来产生终结符,并在正确的上下文中。
单调语法和上下文相关语法时同样强大的:每一种可以由单调语法生成的语言,都可以由上下文相关语法生成,反之亦然。但它们都不如0型语法强大,也就是说,可以由0型语法可以生成任何一种1型语法都无法生成的语言。但奇怪的是没有这样的语言被人们所知道。虽然0型语法和1型语法的区别是基础层面的,而且不是Chomsky先生一时兴起的,它们之间差异的语法太复杂而不能写下来;而只能证明这差异的存在(例如Hopcroft and Ullman [391, pp. 183-184], 或 Révész [394, p. 98])。
当然任何类型的1型语法都属于0型语法,因为1型语法是在0型语法的基础上,增加了一些限制条件推导而来。但如果将1型语法也称为0型语法就会引起混乱;就像把猫叫做哺乳动物一样:正确但不精确。一种语法是按照最小适用类型来命名的(也就是,最高类型数)。
我们可以看到语言t,d&h,先由0型语法生成,也可以由1型语法生成。我们应当也能知道同样还有2型和3型语法适用,但没有4型语法。所以我们说语言t,d&h是一种3型语言,经过限制层数最多(最简单和适合)的语法之后。关于此的一些推论:一个n型语言可以由n型语法或更强大的语法生成,但不能由比较弱小的n+1语法生成;以及:如果一种语言是由n型语法生成,那并不意味着(更弱小的)n+1型语法无法生成它。t,d&h语言的0型语法是一个严格的例子,而只是为了演示目的。
2.3.1.2 构建一个1型语法
1型语法的标准例子就是包含相同数目的a,b,c的集合,按照以下顺序:
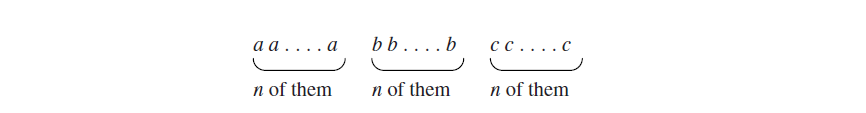
为了完整起见,以及展示1型语法如何被书写出来,如果够聪明的话,我们现在应该得出这个玩具语言的语法。从最简单的例子开始,我们有了以下规则:
0、S ---> abc
获得了S的一个实例,我们可能会想要在开头追加更多的a;如果我们想要记住已经有多少了,那同时我们就应该附加一点东西在结尾处,而且不能是一个b或者c。我们应该使用一个目前未知的符号Q。追加后的规则如下:
1、S ---> aSQ
如果我们用该规则,例如,使用三次,我们就得到下列句子形式:
aaabcQQ
现在,若要从这中间获得aaabbbccc,每一个Q必须等同于一个b和一个c,如预期,但我们不能这么写:
Q ---> bc
因为这会导致第一个c后面是b。因此,如果限定更换只允许在左边是b右边是c的情况下发生,那上述规则就是可行的。新插入的bc就不会造成影响,如下:
2、bQc ---> bbcc
不过,我们不能应用此规则,因为通常Q是在c的右边。可以通过允许Q向左跳过一个c来纠正:
3、cQ ---> Qc
现在,我们可以完成我们的推导:

应该指出的是,上述推导只显示语法能生成正确的字符串,读者需要说服自己,语法不会生成别的东西或不正确的字符串(问题2.4)。
语法总结为了图Fig 2.7。因为a3b3c3的推到图已经相当笨拙,

所以图Fig 2.8给出了a2b2c2的推到图。

语法是单调的,因此属于1型。可以证明这个语言不符合2型;见2.7.1节。
虽然只有上下文相关的1型语法拥有被称为上下文相关语法(CS语法)的权利,但这个名字经常被使用在单调1型语法上。对于单调语法没有标准缩写,但MT可以用来代替。