4.1.1 不含ε规则和循环的Unger解析方法

为了了解Unger方法如何解决解析问题，让我们举一个小例子。假设我们有一个语法规则：

S → ABC | DE | F

并且我们想知道S是否推导出输入句子pqrs。然后初始解析问题可以用如下示意图来表现：

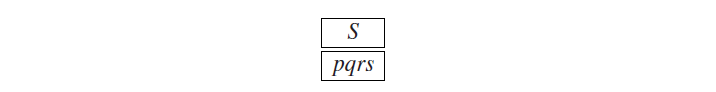
对于每个手册，我们必须首先生成输入的所有可能的分区。生成分区并不难：如果我们有m个杯子，编号从1到m，有n个大理石，编号从1到n，我们必须找到所有的分区，使得一个杯子至少装有一个大理石，每个杯子中大理石的编号都是连续的，并且小编号杯子所含大理石编号比大编号杯子所含大理石编号要小。我们这样来做：首先我们将1号大理石放在1号杯子里，然后将其余的n-1个大理石和m-1个杯子全部分区。这就让我们有了全部的分区，在第一个杯子中有且只有大理石1的情况。接下来，我们把大理石1、2放在第一个杯子中，然后在对剩下的n-2个大理石和m-1个杯子进行分区，如此继续下去。如果n小于m，则不存在分区。

划分输入相当于用杯子（右侧的标志）来划分大理石（输入符号）。如果一个右侧有比句子更多的符号，那就找不到任何分区（没有ε规则）。对于右侧的第一个标志，那分区则必须像以下这样：

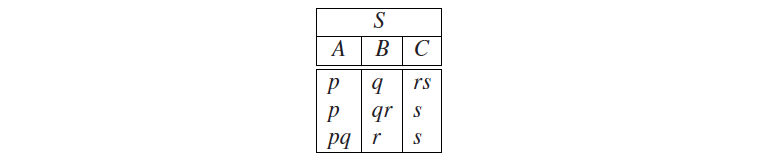
第一个子分区产生了以下子问题：A是否派生出p，B是否派生出q，C是否派生出rs？这些问题的答案都必须是肯定的，否则分区就是错误的了。

对于第二个右侧，我们得到以下分区：

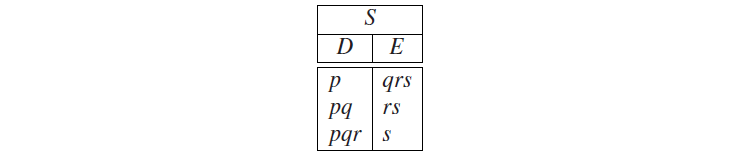
对于最后一个右侧，可以得到以下分区：

所有这些子问题都涉及到较短的句子，除了最后一个。它们都将导致类似的拆分，到最后许多都会失败因为右侧的终结符无法与对应部分的分区相匹配。唯一会引起关注的分区是最后一个。它和我们开始的那个一样复杂。这就是我们不允许语法中存在循环的原因。如果语法中存在循环，我们可能就得一次又一次的重复原来的问题。例如，如果上面的示例中存在一个F→S的规则，那一定会出现这种情况。

以上说明我们这里有一个搜索的问题，我们可以用深度优先搜索或者广度优先搜索技术（见3.5.2节）来解决它。Unger方法使用深度优先搜索来解决。

在接下来的讨论中，图4.1的语法将作为一个例子。这个语法代表了简单的算数表达式语言，包括运算符**+和×，以及运算数i**。

我们将使用句子**(i+i)×i**作为输入示例。因此最初的问题就表现为：

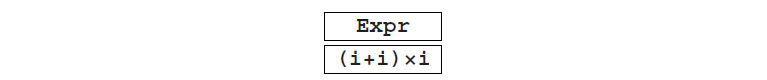
将Expr的第一个替代项写入**(i+i)×i**的输入，得到一个15个分区的表，见图Fig4.2。在这里我们不对全部进行讨论，虽然算法的优化版本需要这样做。我们只讨论至存在一点成功机会的部分：我们先去掉所有与右侧终结符不匹配的部分。因此，值得我们关注的部分就剩了：

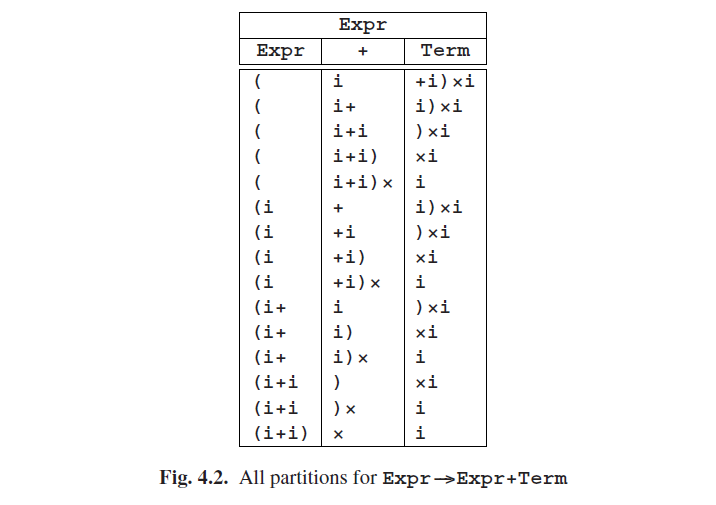
这里面临的第一个问题就是找出是否匹配，如果匹配，那么Expr如何推导出**(i**。我们不能把**(i分解成三个非空部分，因为它只包含两个符号。因此，我们唯一可以应用的规则是Expr--->Term**。同样，接下来我们能用的规则是Term--->Factor。所以现在我们有了：

然而这是不可能的，因为第一个右侧的因子有太多符号，而第二个仅包含一个终结符。因此，我们开始使用的部分并不合适，应该被排除掉。而其他部分已经被排除了，所以我们可以得出结论，规则Expr--->Expr+Term无法派生出输入。

Expr右侧的第二部分包含一个符号，因此我们这里只有一个分区，由一个部分组成。将此部分为Term的第一个右侧进行划分又会产生15种情况，其中又只有一个又成功的可能：

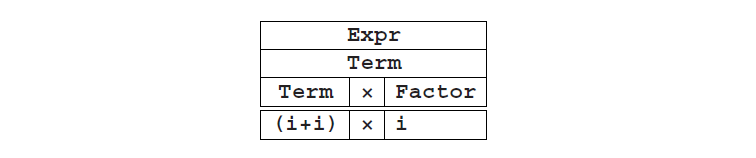
继续我们的探索，我们将得到以下派生结果（唯一的派生）：

这个例子展示了这个方法的几个方面：即使是小的例子也需要庞大的工作量，不过稍微进行检查就可以省掉大量的无用功。例如，将右侧的符合与分区进行搭配通常会导致分区被拒绝，因此无需进行下步操作。Unger[12]提出了几个更多的检查点。例如，可以计算每个非终端派生的终端符号字符串的最小长度。一旦知道某个非终结符只能派生出长度为n的终结符字符串，则可以立即排除长度小于这个长度的非终结符分区。