3.9 传递闭包
解析中的许多算法(以及在计算机科学中的许多其他分支)都具有一些从初始信息开始的属性,然后根据一些理论规则推到得出结论,一直到不能得出更多的结论为止。在2.9.5.1 和2.9.5.2 节中的推理规则中, 我们已经看到了两个例子。这些推理是完全不同的,并且一般的推理规则可以是任意复杂的。为了得到一个清晰的计算结论的算法,闭包算法,我们现在将考虑一个最简单的可能的推理规则: 传递性。这种规则的形式如下:
如果AB 并且BC 那么AC
其中是任意符合规则的操作符。最明显的是=,但是<和以及其他许多也是可以的。但是(不等于)却不是的。
作为一个例子,我们将考虑一个非终结符的“左角集”的计算。一个非终结符B在一个非终结符A的左角集中,如果有一个派生AB···,知道这点有时是有用的,因为在其他方面来说,任何B可以开始的字符A也都能开始。
有下面这样一个语法

我们如何才能找出C在S的左角集中?语法中的规则SST和SAa立即就让我们知道S和A在S的左角集中。我们把这写作S∠S和A∠S,其中∠代表左角。这同样告诉我们A∠T,B∠A,还有C∠B。这是我们的初始信息(图3.19(a))。

现在很容易看出,如果A在B的左角集中,B在C的左角集中,那么A也在C的左角集中。公式如下:
A∠B ∧ B∠C A∠C
这是我们的推理规则,而且我们将使用它来得出新结论或“推论”,通过两两组合已知的事实来产生更多的已知因子。然后通过应用推理规则直到不再产生新的因子来获得传递闭包。在传递闭包的上下文中,因子也被称为“关系”,虽然一般∠是(二进制)关系,并且A∠B和B∠C 是关系的 "实例"。
通过图 3.19 (a) 中的列表,我们首先将S∠S和S∠S结合起来。这将产生S∠S,这是相当令人失望的因为我们已经知道了;它在图 3.19 (b) 中, 标有一个**√, 以表明它不是新的。(S∠S, A∠S的)结合产生A∠S**,但是我们也已经知道了。没有其他的因子与S∠S结合,所以我们继续看A∠S,而这得到了A∠S和B∠S;第一个我们已经知道了,但是第二个是第一次被我们知道。接着(A∠T,B∠A)就得到了B∠T,等等,做完剩下部分的第一轮结果见图3.19(b)。
第二轮结合了三个有新有旧的因子。第一个是发现由A∠S和C∠A (c)得到了C∠S,第二个发现是C∠T。
第三轮将(c)中的两个新因子与(a),(b),(c)中的结合起来,但没有发现新的因子;所以这个算法最终发现了10个因子。
请注意,我们已经在这个初级算法中实现了一次优化:基础算法将启动第二轮甚至更多轮次,通过将已知的所有因子之间配对,而不仅仅只是在新发现的因子之间。
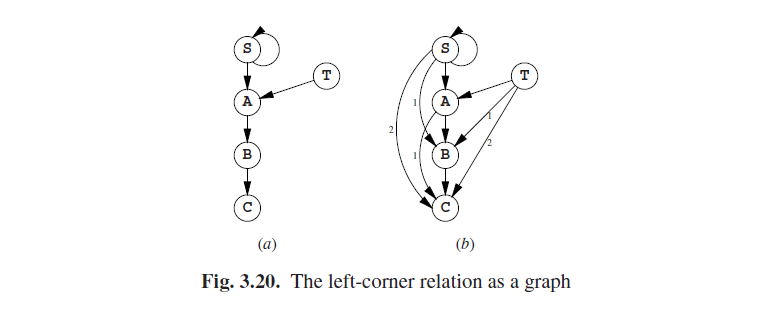
在一个图中用弧线表示因子或关系通常是有帮助的。最初的情况见图3.20 (a),最终的结果见(b)。箭头旁边的数字表明得到该因子经过了几轮计算。
闭包算法的效率很大程度上依赖于它所所使用的推理算法,而传递规则的情况被广泛的进行了研究。传递闭包主要有三种方法来进行:初级版、普通版和高级版;我们将简要的对每一种进行介绍。上面描述过的初级算法,在通常情况下往往是相当有效率的,但会画出一张很大的图,而且特殊情况下可能会需要计算很多轮。同样它还会重复计算很多次,我们可以在图3.19中看出;15个结果中有10个是已经得到了的。但考虑到“正常”语法的大小,初级算法几乎可以满足所有情况下的解析。
普通的进行传递闭包的方式是使用Warshall的算法[409]。其优势是非常简单实现,而且它需要的时间仅取决于图中N节点的数量而不是弧线的数量,但它的缺点是总是需要*O(N3)*的时间。这回让它在和其他任何闭包算法的比较中总是输掉。
高级算法避免了导致初级算法效率底下的劣势:1.图中的圆圈被收敛为“强联通分量”;2.弧线以一种顺序组合起来,并允许弧线进行复制而不是重复计算;3.使用更有效的数据表示。例如,一个高级算法首先会计算从A的所有输出弧,然后将之拷贝至T而不是重新计算一次。Tarjan [334] 描述了第一个高级可传递闭包算法。并在其他很多刊物上广泛转载;见Nuutila[412]和互联网。它需要的时间与其最终得出的结果数量成正比。
高级可传递闭包算法在大型应用程序 (数据库等) 中非常有用,但它在解析中的位置确实令人怀疑的。一些作者建议在LALR解析器生成器中使用它们,但应该在非常庞大的语法上使用,以保证算法的复杂性有一个很好的回报。
强调算法的闭包性质的优点可以让人集中于推理规则,并将底层的闭包算法当做理所当然;这对于算法设计很有帮助。然而大多数的解析算法都很简单,以至于不需要分解成推理规则和闭包解释。因此我们将仅在有助于理解的地方使用推理规则(9.7.1.3节),以及当其原本就是语法的一部分的情况下使用(7.3节,图表解析)。对于其余的我们将简单的讲述算法,然后指出他们是传递闭包算法得出的。