4.2.6 消除CNF转换的影响
从图4.6的语法和图4.16的识别表中,我们不难发现识别表包含了原始语法中大部分非终结符的我们所需的信息。但是有一少部分非终结符没有在识别表中:Scale,Real和Empty。Scale和Empty可以不关注,因为没有ε规则后,它们就变成了死胡同。Empty也可以完全不管,因为它只能生成空的句子。而Scale由Scale'替换,因为Scale和Scale'生成的几乎一模一样,除了空字符串。我们可以用它来向识别表添加更多信息:每当出现Scale',我们就添加一个Scale。
非终结符Real被删除了,因为没有单元规则之后就变得无法到达了。不过现在CYK算法并没有要求语法中的所有非终结符都是可到达的。所以我们也可以把Real留下,然后将它的规则转换成CNF。接下来当合适的时候,CYK算法将会把Real添加到识别表中。Real被添加到图Fig4.15的语法的规则将会是如下:
Real ---> N1 Scale’ | Integer Fraction
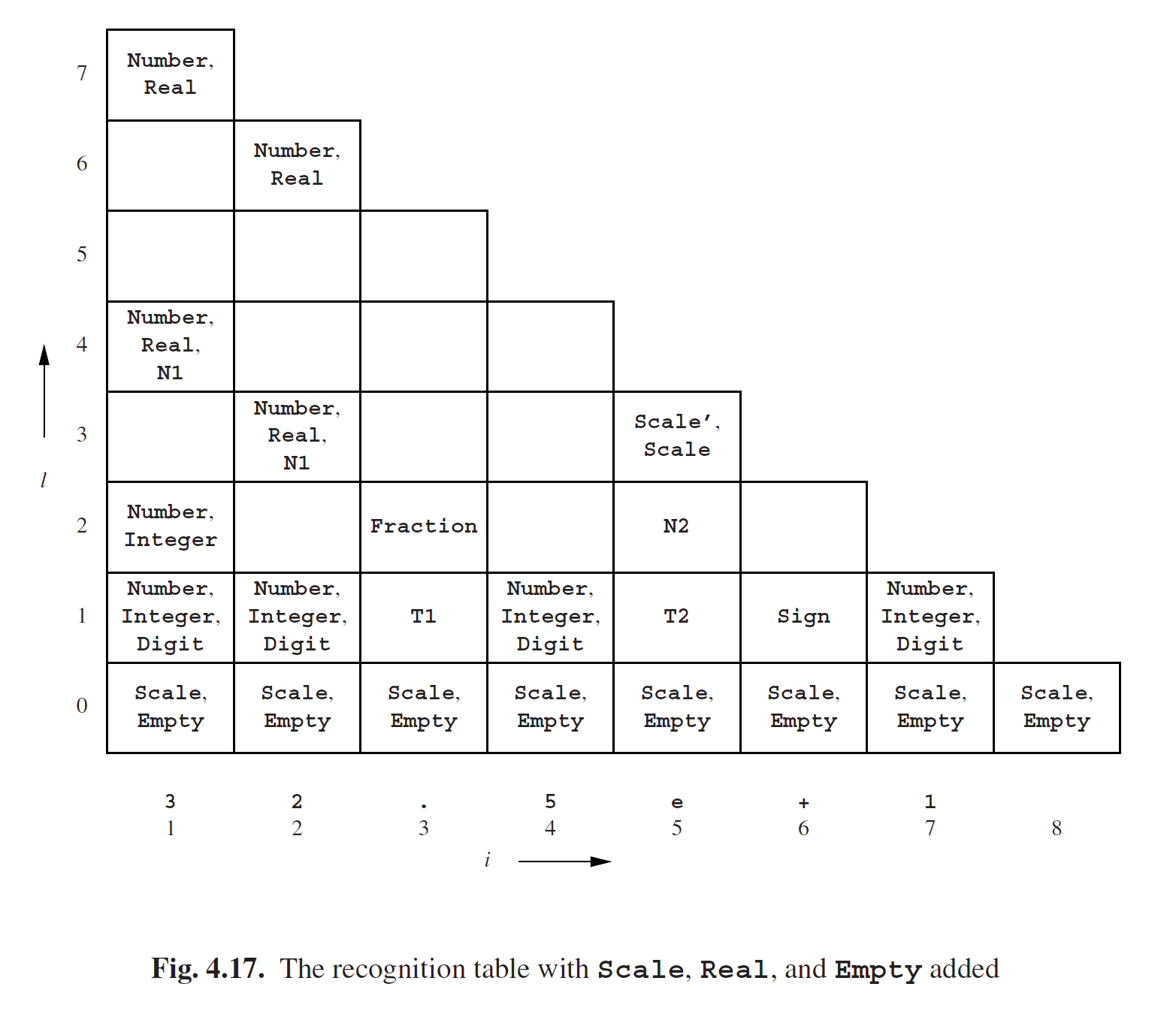
生成的识别表如图4.17所示。 在这个图中,我们也在底部添加了额外的一行。这一行是生成了空字符串的非终结符。这些非终结符可能出现在句子的任意两个符号之间,也可能出现在句子头或句子尾。集合*Ri,0包含出现在符号ti前面的非终结符,而集合Rn+1,0*包含出现在句子后面的非终结符。
现在我们就有了一个包含了所有我们解析原始语法中句子的所需信息的识别表。同样,从起始符S开始生成。如果A1A2 · · ·Am是S的右侧,我们来看看这个规则是不是也适用,也就是说A1A2 · · ·Am是否能生成s1,n。确定之后就从A1。有两种情况:
-
A1为终结符。在这种情况下,它必须是s1,n的第一个符号,否则此规则将不适用。接下来,我们要核对A2 · · ·Am是否能生成s2,n-1,用我们核对*A1A2 · · ·Am是否能生成s1,n*相同的方式。
-
A1为非终结符。在这种情况下,它必须是R1,k(部分k值)的一个值,否则这个规则将不适用。接下来我们要核对A2 · · ·Am是否能生成sk+1,n-k,以我们核对A1A2 · · ·Am是否能生成s1,n相同的方式。如果我们想要所有的解析,我们必须对每一个不同k取值的R1,k包含的A1都进行这个操作。请注意对于生成空字符串的所有非终结符都不存在任何问题,因为对于所有i值它们都属于Ri,0。
到此我们就已经确定了规则是否适用了,适用的话,那部分规则生成那部分子句也已经确定了。接下来就要确定是如何生成的子句了。这个任务和我们刚开始时候的任务很像,解决方法也是类似的。这个过程只会持续一段时间,如果语法中不包含循环。这就是一个Unger解析器,在开始之前就已经区分出了能完成解析的部分。
让我们回到图Fig4.6的语法和图Fig4.17的识别表,看看如何在我们的示例句子中起作用。现在我们已经知道Number可以生成32.5e+1,但并不知道是如何生成的。首先我们看看:Number--->Integer规则有用吗?Integer是*R1,1和R1,2的子集,但除了Integer之外没有其他能生成句子其他部分的规则,所以这个不对。那Number--->Real规则对不对呢?对了,就是它!因为Real是R1,7*的值,而句子的长度也是7.因此我们的生成过程从以下开始:
Number ---> Real ---> · · ·
现在对于非终结符Real我们也遇到了基本一样的问题:那Real ---> Integer Fraction Scale是不是有用呢?Integer是*R1,1的值,但在任何一个R2,k集合中都找不到Fraction。不过,Integer是R1,2的值,而且Fraction是R3,2的值。但是,Scale是R5,0的值,而这没用,因为它不能为其他生成带来任何规则。不过好在,Scale还是R5,3*的值,而这与句子的结尾正好相合。所以我们可以确定这个规则是实实在在适用的,那我们继续我们的生成:
Number ---> Real ---> Integer Fraction Scale ---> · · ·
现在句子分成了三部分:

找到唯一的生成就留给读者了,就在下面:
