3.1.2 各种模糊性
一个语法产生的句子可以很容易拥有多于一个的生成树,既,很容易有多于一种的方式来生成一个句子。从形式角度来看,这不是大问题(一个集合不会计算它包含了一个元素多少次),但是只要我们对语义感兴趣,那这差别就很重要了。不足为奇的是,拥有多个生成树的的句子被称为模糊性,但是我们必须立即区分本质的模糊性和貌似的模糊性。差异来源于我们对生成树本身并不感兴趣的事实,而更感兴趣于它们所描述的语义。一个歧义句是貌似模糊性的,如果它的所有的生成树都描述同样的语义;如果部分语义不不同,其模糊性就是本质的。“模糊”的概念也可以用来定于语法:语法是本质模糊的如果它可以生成一个本质模糊的句子,是貌似模糊的如果它能生成一个貌似模糊的句子(但不是一个本质上模糊的),以及是非模糊性的如果都不能生成的话。一个语法的可能模糊性测试,间9.14节。
图Fig 3.1给出了一个简单的模糊性语法。注意规则2不同于图Fig 2.30中的。

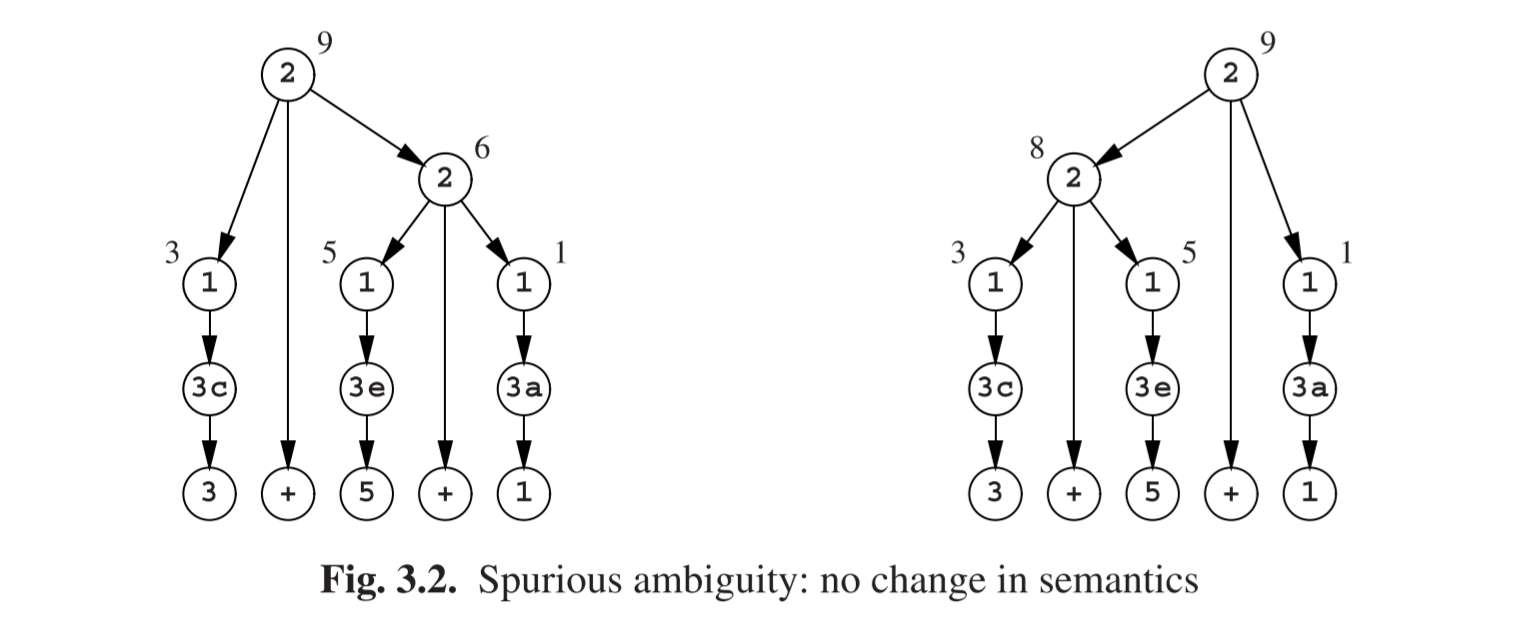
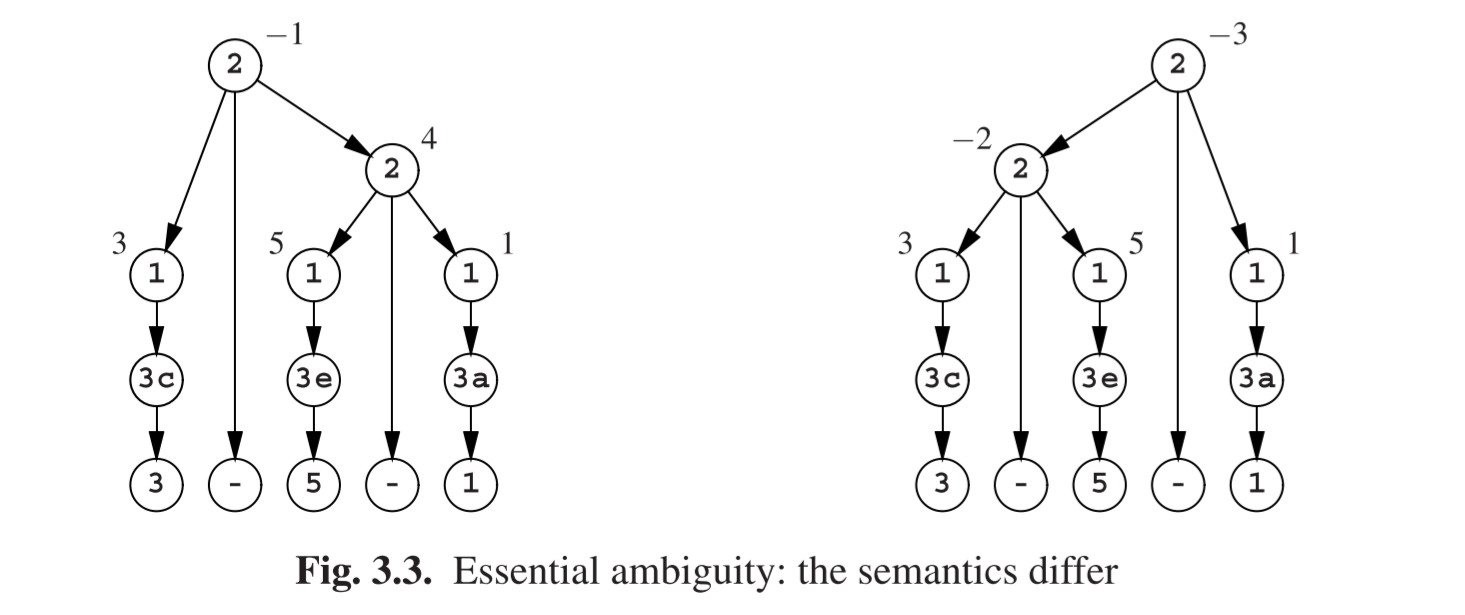
现在3+5+1有了两个生成树(图Fig 3.2),但是两者的语义是一样的:9。模糊性是不确定的。然而如果我们把**+变成-,那其模糊性就是本质的了,如图Fig 3.3。图Fig 2.30的非模糊性语法,当+变成-**后,依旧是非模糊性,并且保持正确的语义。
奇怪的是,语言也可以是模糊性的:(上下文无关)语言,其语法没有非模糊性的。这样的语言是固有模糊性的。语言L = ambncn ∪ apbpcq就是一个例子。L中的句子要么由一些a后接着一组嵌套的b和c的序列组成,要么由一些c后接着一组嵌套的a和b的序列组成。例句:abcc,aabbc,还有aabbcc**;abbc是一个非句子例子。L由图Fig 3.4的语法生成。

直观的说,为什么L是模糊性的是相当清晰的:语法的任何可以生成ambncn的部分都无法避免生成anbncn,并且任何可以生成apbpcq的部分都无法避免生成apbpcp。所以无论我们做什么,与a,b,c数字相等的形式将总是会被生成两次。但真实的证明确实无法做到,这不是本书范围之内的东西了。