2.10 设定上下文无关和正则语言的属性
由于语言是集合,所以很自然会问到集合的标准操作——并集、交集和补集(补充)——是否能用在语言上,如果可以,要怎么做。
S1和S2的并集包含两两个集合中的全部元素;写作S1∪S2。交集包含了两个集合中的共同元素;写作S1∩S2。S的补集包含了属于Σ但不属于S的元素;写作$$\rightharpoondown$$S*。在形式语言的上下文中,这些集合是通过语法定义的,所以实际上我们是想要对语法进行操作,而不是语言。
为两种语言的并集构建语法,对上下文无关和正则语言来说是繁琐的(实际上对所有Chomsky类型都是):仅仅构建一个新的起始符号S'→S1|S2,*S1和S2*是描述两种语言的语法的起始符号。(当然,如果我们想结合两种语言成为一种新的,那我们必须确保他们之中的名字是不同的,不过这是很容易的事情。)
然而交集是另一回事,因为两个上下文无关语言的交集并不一定是上下文无关的,如以下示例所示。有两个语言L1 = anbncm和L2 = ambncn,他们由CF语言描述
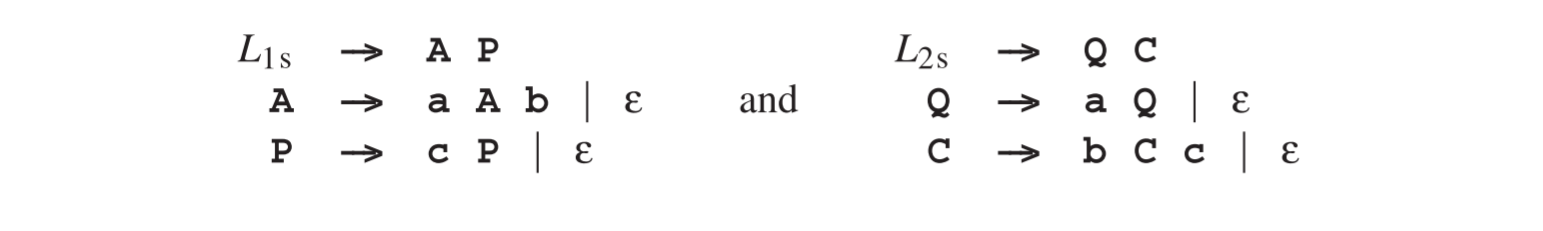
当我们拿到一个同时属于两个语言的字符串放入交集时,就有了**apbqcr这种形式,而由于L1和L2其中p = q以及q = r。所以交集中包含anbncn**这样形式的字符串,而我们知道这样的语言不是上下文无关的(见2.7.1节)。
CF语言的交集有一些奇特的属性。第一,两个CF语言的交集总是有一个1型语法——但这个语法却不容易构建。更值得注意的是,三个CF语言的交集比两个的交集要强大的多:Liu 和 Weiner[390]表明,可以获得k个CF语言的交集,而不是k-1个。除此之外,任何1型语言,甚至任何0型语言,可以通过两个CF语言的交集来构建,我们就能擦除结果字符串中的所有属于可擦除符号集中的符号。
我们将用来演示这个惊人现象的CS语言,是由两个相同部分的句子组成的集合:ww,w是给定字符集中的任何字符串;例如aa和abbababbab。用来相交的两个语言由以下定义:

其中x和y是可擦出符号。第一个语法生成的字符串由三个部分组成,a和b的序列A1,其次是其“黑暗镜像”M1,a对应x,b对应y,再接着是a和b的一个任意序列G1。第二个语法生成的字符串包含,a和b的一个任意序列G2,一个“黑暗”序列M2以及它的镜像A2,其中再次a对应x,b对应y。交集强制A1 =G2, M1 =M2,and G1 =A2。这使得*A2成为了A1镜像的镜像,同理A1*也是这样。交集中的一个句子示例如abbabyxyyxabbab,我们可以看到其镜像abbab和yxyyx。现在我们擦除可擦除符号x和y,就得到了最后的结果abbababbab。
通过使用应用上述镜像,就能够很简单的证明任何0型语言能够通过两个CF语言的交集,加上一组可擦除符号来构建了。详细介绍,见Révész [394]。
注意,一个上下文无关和一个正则语言的交集,一般都是一个上下文无关语言,并且,有一个相关的简单算法来为这个交集语言构建一个语法。这让非凡的解析算法得到了增长,浙江在13章进行讨论。
如果我们不能得到两个CF语言的交集,并且仍处于CF语言中,那我们肯定不能得到一个CF语言的补集并仍在CF语言中。如果我们能得到,我们就能得到两个语言的补集,让后取其交集然后在取其补集,最后就得到它们的补集。公式:L1 ∩ L2 = $$\rightharpoondown$$(($$\rightharpoondown$$L1) ∪ ($$\rightharpoondown$$L2));这个公式就是大家熟知的De Morgan定律(De Morgan’s Law)。
在5.4节我们将会看到正则(3型)语言和正则语言的并集,交集和补集。
有趣的是推测一下将会有什么发送,如果形式语言是基于集合理论,一开始就使用所有的集合操作,而不是Chomsky层次理论。那么上下文无关语言还会被发明么?