6.4 左递归的消除

我们先讨论消除直接左递归的方法。假定ε规则和单元规则已经被消除了（见4.2.3.1节和4.2.3.2节）。现在，使A为一个左递归规则，并且

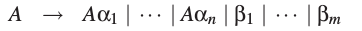
是A拥有的所有规则。没有等于ε的α_i，否则我们会有A→A规则和一个单元规则。也没有等于ε的β_j，否则会有一个ε-规则。由A生成的句型只用*A→Aα_k*规则，这些句型都有这样的形式：

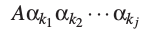
并且当A→β_i规则使用时，句型不再以A开头，对一些i，和一些k₁,...,k_j,它有如下的形式：

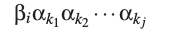
这里j可能为0.同样的句型也可以用如下规则生成：

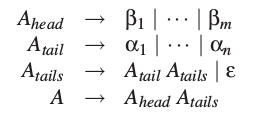
或者，不重新引入ε规则生成的话就是这样：

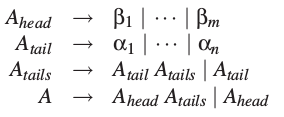
这里A_head,A_tail和A_tails是新引入的非终结符。所有α_i都不是ε类型，所以A_tail不会推导出ε，所以A_tails不是左递归。不过A可能仍然是左递归的，但不是直接左递归，因为没有β_j是以A开始，然而它们却可能推导出以A开始的句型。

一般来说，消除间接左递归要更复杂。思路就是先将非终结符标号，标为A₁,A₂,...,A_n。那么，对一个左递归非终结符A，就有如下推导

任何时刻句型的最左边都是非终结符，然后每次使用其中一个右侧替代。每一个非终结符都有一个标号，计作i₁,i₂,...,i_m，于是在推导中我们得到了这么一串数：i₁,i₂,...,i_m,i₁。现在，如果我们没有任何包含jα(j≤i)的规则A_i→A,那这就是不存咋的，因为*i₁<i₂<...<i_m<i₁*是不存在的。

现在就要消除这种形式的规则。我们从A₁开始。对A₁，要消除了只是直接递归的规则，我们已经看到了应该怎么做。接着轮到A₂。每一个有着A₂→A₁α形式的产生式都要被替代成如下：

这里*A₁*的规则为

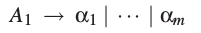
这不可能产生A₂→A₁γ形式的新规则，因为我们已经消除了A₁的左递归规则，而且α_i都不为ε。接着，我们来处理A₂的直接左递归规则。这样对A₂的工作就结束了。同样，我们对A₃到A_n进行处理，按照总是先替代A_i→A₁γ,再A_i→A₂δ等的顺序。我们必须按照这样的顺序，因为替换一个A_i→A₂δ的规则可能会引入一个A_i→A₃γ规则，而不是A_i→A₁α规则。