6.1 仿最左推导
现在让我们用一个例子解释这样一个推导过程。如图Fig6.1所示语法。这个语法生成与a和b数量相同的句子。

让我们从开始符号S开始尝试解析句子aabb。S是我们的第一个预测.我们的预测的第一个符号是非终结符,所以我们要用它的一个右侧替代它。在这个语法中,S有两个选择:我们或者用规则S→aB,或者用规则S→bA。句子从a开始而不是b,所以这里我们不能用第二个规则。应用第一个规则我们得到预测aB。现在预测的第一个字符是一个终结符。因此,我们别无选择:
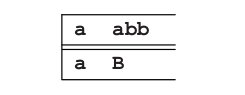
我们要将这个字符和句子的当前字符做匹配,这里当前字符也是a。因此我们获得了一个匹配项,并接受a。余下的句子就留给我们一个预测B:abb。预测的第一个字符又是一个非终结符,所以要被它的一个右侧代替。现在我们有三种选择。然而,第一和第二个选择在这里不适用,因为它们由b开始,但实际上我们需要的是a。所以,我们采用第三个选择,现在我们有了预测aBB:
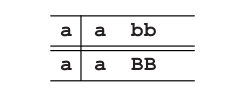
因此对于当前输入字符我们再次有了一个匹配项,所以我们接受它,然后继续bb的预测BB。我们要再次用其右侧替代其最左的B。句子的下一个字符是b,所以这里第三个选择不适用。这仍然留给我们两个选择:b和bS。所以我们可以两个都尝试,但也可以用更聪明一点的方法。如果我们采用bS,我们至少会得到一个额外的a(由于S),所以这不可能是正确的选择。因此我们只能选择b,于是得到了对应bb的预测bB。我们再次得到了一个匹配项,这留给我们b的预测B。由于同样的原因,我们选择b。匹配之后,我们的预测为空。幸运的是,我们同时到达了输入句子的末尾,所以我们接受了这个输入。如果我们记录下了使用过的生成规则,就能得到下面的推导过程:
S→aB→aaBB→aabB→aabb
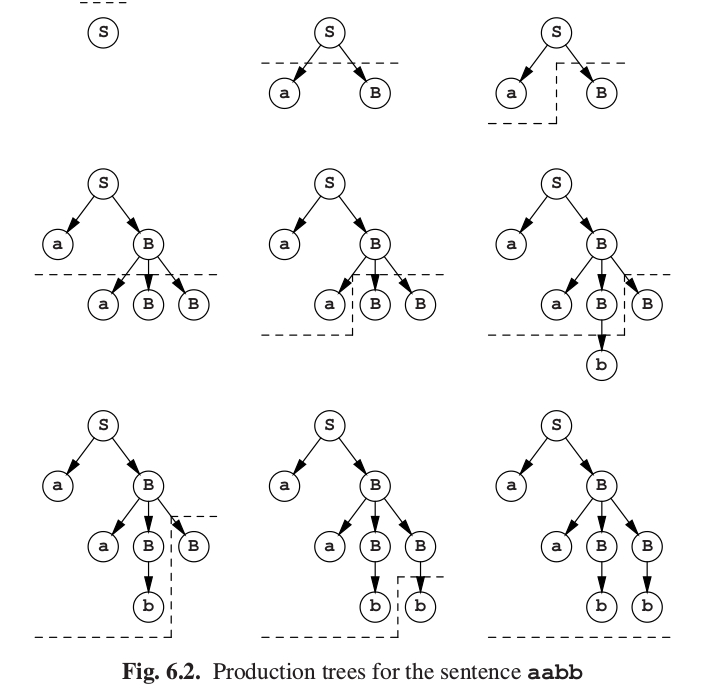
图Fig6.2用树的形式展现了解析的步骤。图中的虚线将已经处理过的部分和未处理部分分开。整个过程中,预测的最左侧符号都经过了处理。
这个例子显示了本章讨论的解析器的几个共同点:
-
我们总是对预测中的最左符号进行处理
-
如果这个符号是终结符,我们就没有其他选择:我们只能将它和当前的输入字符匹配,或者直接拒绝解析
-
如果这个符号是非终结符,我们需要采用一个预测:它需要被它的一个右侧替代。因此,我们总是先处理预测中的最左符号,从而得到了最左推导。
-
所以,自顶向下方法将解析树的节点用前序组织:父节点总是在它的子节点之前被识别。